Nested Logit and Non-Proportional Patterns of Substitution

%load_ext autoreload
%autoreload
import arviz as az
import matplotlib.pyplot as plt
import pandas as pd

from pymc_marketing.customer_choice.nested_logit import NestedLogit
from pymc_marketing.paths import data_dir
from pymc_marketing.prior import Prior

az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = [12, 7]
plt.rcParams["figure.dpi"] = 100

We’ve seen how the Multinomial Logit model suffers from the IIA limitation that leads to implausible counterfactual inferences regarding market behaviour. We will show how the nested logit model specification avoids this property by adding more explicit structure to the choice scenarios that are modelled.

In this notebook we will re-use the same heating choice data set seen in the Multinomial Logit example and apply a few different specifications of a nested logit model.

data_path = data_dir / "choice_wide_heating.csv"
df = pd.read_csv(data_path)
df

	idcase	depvar	ic_gc	ic_gr	ic_ec	ic_er	ic_hp	oc_gc	oc_gr	oc_ec	oc_er	oc_hp	income	agehed	rooms	region
0	1	gc	866.00	962.64	859.90	995.76	1135.50	199.69	151.72	553.34	505.60	237.88	7	25	6	ncostl
1	2	gc	727.93	758.89	796.82	894.69	968.90	168.66	168.66	520.24	486.49	199.19	5	60	5	scostl
2	3	gc	599.48	783.05	719.86	900.11	1048.30	165.58	137.80	439.06	404.74	171.47	4	65	2	ncostl
3	4	er	835.17	793.06	761.25	831.04	1048.70	180.88	147.14	483.00	425.22	222.95	2	50	4	scostl
4	5	er	755.59	846.29	858.86	985.64	883.05	174.91	138.90	404.41	389.52	178.49	2	25	6	valley
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
895	896	gc	766.39	877.71	751.59	869.78	942.70	142.61	136.21	474.48	420.65	203.00	6	20	4	mountn
896	897	gc	1128.50	1167.80	1047.60	1292.60	1297.10	207.40	213.77	705.36	551.61	243.76	7	45	7	scostl
897	898	gc	787.10	1055.20	842.79	1041.30	1064.80	175.05	141.63	478.86	448.61	254.51	5	60	7	scostl
898	899	gc	860.56	1081.30	799.76	1123.20	1218.20	211.04	151.31	495.20	401.56	246.48	5	50	6	scostl
899	900	gc	893.94	1119.90	967.88	1091.70	1387.50	175.80	180.11	518.68	458.53	245.13	2	65	4	ncostl

900 rows × 16 columns

Single Layer Nesting

The important addition gained through the nested logit specification is the ability to specify “nests” of products in this way we can partition the market into “natural” groups of competing products ensuring that there is an inherent bias in the model towards a selective pattern of preference. As before we specify the models using formulas, but now we also add a nesting structure.

## No Fixed Covariates
utility_formulas = [
    "gc ~ ic_gc + oc_gc | income + rooms ",
    "ec ~ ic_ec + oc_ec | income + rooms ",
    "gr ~ ic_gr + oc_gr | income + rooms ",
    "er ~ ic_er + oc_er | income + rooms ",
    "hp ~ ic_hp + oc_hp | income + rooms ",
]


nesting_structure = {"central": ["gc", "ec"], "room": ["hp", "gr", "er"]}


nstL_1 = NestedLogit(
    df,
    utility_formulas,
    "depvar",
    covariates=["ic", "oc"],
    nesting_structure=nesting_structure,
    model_config={
        "alphas_": Prior("Normal", mu=0, sigma=5, dims="alts"),
        "betas": Prior("Normal", mu=0, sigma=1, dims="alt_covariates"),
        "betas_fixed_": Prior("Normal", mu=0, sigma=1, dims="fixed_covariates"),
        "lambdas_nests": Prior("Beta", alpha=2, beta=2, dims="nests"),
    },
)
nstL_1

<pymc_marketing.customer_choice.nested_logit.NestedLogit at 0x177955f90>

We will dwell a bit on the manner in which these nests are specified and why. The nested logit model partitions the choice set into nests of alternatives that share common unobserved attributes (i.e., are more similar to each other). It computes the overall probability of choosing an alternative as the product of (1) The probability of choosing a nest (marginal probability), and (2) the probability of choosing an alternative within that nest (conditional probability, given that nest). In our case we want to isolate the probability of choosing a central heatings system and a room based heating system.

Each of the alternatives alt is indexed to a nest. So that we can determine (§) the marginal probability of choosing room or central and (2) conditional probability of choosing ec given that you have chosen central. Our utilities are decomposed into contributions from fixed_covariates and alternative specific covariates:

\[ U = Y + W + \epsilon \]

and the probabilities are derived from these decomposed utilitiies in the following manner.

\[ P(i) = P(\text{choose nest B}) \cdot P(\text{choose i} | \text{ i} \in \text{B}) \]

where

\[ P(\text{choose nest B}) = \dfrac{e^{W + \lambda_{k}I_{k}}}{\sum_{l=1}^{K} e^{W + \lambda_{l}I_{l}}} \]

and

\[ P(\text{choose i} | \text{ i} \in \text{B}) = \dfrac{e^{Y_{i} / \lambda_{k}}}{\sum_{j \in B_{k}} e^{Y_{j} / \lambda_{k}}} \]

while the inclusive term \(I_{k}\) is:

\[ I_{k} = ln \sum_{j \in B_{k}} e^{Y_{j} / \lambda_{k}} \text{ and } \lambda_{k} \sim Beta(1, 1) \]

such that \(I_{k}\) is used to “aggregate” utilities within a nest a “bubble up” their contribution to decision through the product of the marginal and conditional probabilities. More extensive details of this mathematical formulation can be found in Kenneth Train’s “Discrete Choice Methods with Simulation”.

nstL_1.sample(
    fit_kwargs={
        "target_accept": 0.97,
        "tune": 2000,
        "nuts_sampler": "numpyro",
        "idata_kwargs": {"log_likelihood": True},
    }
)

Sampling: [alphas_, betas, betas_fixed_, lambdas_nests, likelihood]

There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
Sampling: [likelihood]

<pymc_marketing.customer_choice.nested_logit.NestedLogit at 0x177955f90>

The model structure is quite a bit more complicated now than the simpler multinomial logit as we need to calculate the marginal and conditional probabilities within each of the nests seperately and then “bubble up” the probabilies as a product over the branching nests. These probabilities are deterministic functions of the summed utilities and are then fed into our categorical likelihood to calibrate our parameters against the observed data.

nstL_1.graphviz()

But again we are able to derive parameter estimates for the drivers of consumer choice and consult the model implications is in a standard Bayesian model.

az.summary(nstL_1.idata, var_names=["betas", "alphas", "betas_fixed", "lambdas_nests"])

/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:596: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:991: RuntimeWarning: invalid value encountered in scalar divide
  varsd = varvar / evar / 4
/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:596: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:991: RuntimeWarning: invalid value encountered in scalar divide
  varsd = varvar / evar / 4

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
betas[ic]	-0.001	0.001	-0.002	-0.000	0.000	0.000	3432.0	3044.0	1.00
betas[oc]	-0.006	0.001	-0.008	-0.003	0.000	0.000	1158.0	1530.0	1.00
alphas[gc]	2.224	2.091	-0.386	6.349	0.081	0.058	720.0	1322.0	1.00
alphas[ec]	2.172	2.077	-0.461	6.309	0.078	0.058	819.0	1279.0	1.01
alphas[gr]	0.121	0.133	-0.124	0.389	0.004	0.003	1417.0	1351.0	1.00
alphas[er]	1.426	0.344	0.826	2.104	0.010	0.006	1235.0	2297.0	1.00
alphas[hp]	0.000	0.000	0.000	0.000	0.000	NaN	4000.0	4000.0	NaN
betas_fixed[gc, income]	-1.879	2.873	-7.858	1.317	0.098	0.109	754.0	1100.0	1.00
betas_fixed[gc, rooms]	-1.192	2.369	-5.704	1.906	0.067	0.106	1365.0	1753.0	1.00
betas_fixed[ec, income]	-1.819	2.835	-7.884	1.253	0.095	0.104	800.0	1072.0	1.00
betas_fixed[ec, rooms]	-1.166	2.344	-5.667	2.029	0.067	0.107	1392.0	1670.0	1.00
betas_fixed[gr, income]	-0.113	0.167	-0.431	0.102	0.005	0.007	1069.0	1693.0	1.00
betas_fixed[gr, rooms]	-0.060	0.134	-0.372	0.116	0.003	0.004	1892.0	2189.0	1.00
betas_fixed[er, income]	-1.049	1.095	-3.247	0.728	0.035	0.026	965.0	1110.0	1.00
betas_fixed[er, rooms]	-0.639	1.008	-2.718	1.032	0.026	0.023	1568.0	1780.0	1.00
betas_fixed[hp, income]	0.000	0.000	-0.000	0.000	0.000	NaN	4000.0	4000.0	NaN
betas_fixed[hp, rooms]	0.000	0.000	-0.000	-0.000	0.000	NaN	4000.0	4000.0	NaN
lambdas_nests[central]	0.815	0.101	0.631	0.987	0.003	0.002	938.0	1600.0	1.00
lambdas_nests[room]	0.615	0.102	0.430	0.797	0.003	0.002	1036.0	1811.0	1.00

Here we see additionally lambda parameters for each of the nests. These terms measure how strongly correlated the unobserved utility components are for alternatives within the same nest. Closer to 0 indicates a high correlation, substitution happens mostly within the nest. Whereas a value closer to 1 implies lower within nest correlation suggesting IIA approximately holds within the nest. The options available for structuring a market can be quite extensive. As we might have “nests within nests” where the conditional probabilities flow through successive choices within segments of the market.

Two Layer Nesting

In this PyMC marketing implementation we allow for the specification of a two-layer nesting representing succesive choices over a root nest and then nests within the child nests.

utility_formulas = [
    "gc ~ ic_gc + oc_gc ",
    "ec ~ ic_ec + oc_ec ",
    "gr ~ ic_gr + oc_gr ",
    "er ~ ic_er + oc_er ",
    "hp ~ ic_hp + oc_hp ",
]


nesting_structure = {"central": ["gc", "ec"], "room": {"hp": ["hp"], "r": ["gr", "er"]}}

nstL_2 = NestedLogit(
    df,
    utility_formulas,
    "depvar",
    covariates=["ic", "oc"],
    nesting_structure=nesting_structure,
    model_config={
        "alphas_": Prior("Normal", mu=0, sigma=1, dims="alts"),
        "betas": Prior("Normal", mu=0, sigma=1, dims="alt_covariates"),
        "betas_fixed_": Prior("Normal", mu=0, sigma=1, dims="fixed_covariates"),
        "lambdas_nests": Prior("Beta", alpha=2, beta=2, dims="nests"),
    },
)
nstL_2

<pymc_marketing.customer_choice.nested_logit.NestedLogit at 0x17d77b760>

nstL_2.sample(
    fit_kwargs={
        # "nuts_sampler_kwargs": {"chain_method": "vectorized"},
        "tune": 2000,
        "target_accept": 0.95,
        "nuts_sampler": "numpyro",
        "idata_kwargs": {"log_likelihood": True},
    }
)

Sampling: [alphas_, betas, lambdas_nests, likelihood]

Sampling: [likelihood]

<pymc_marketing.customer_choice.nested_logit.NestedLogit at 0x17d77b760>

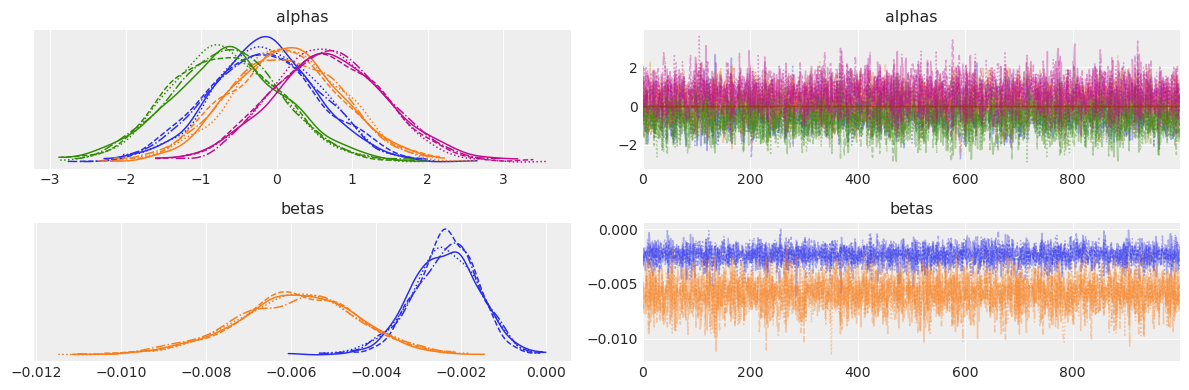
az.plot_trace(nstL_2.idata, var_names=["alphas", "betas"])
plt.tight_layout()

/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/density_utils.py:488: UserWarning: Your data appears to have a single value or no finite values
  warnings.warn("Your data appears to have a single value or no finite values")
/var/folders/__/ng_3_9pn1f11ftyml_qr69vh0000gn/T/ipykernel_60237/28403481.py:2: UserWarning: The figure layout has changed to tight
  plt.tight_layout()

az.summary(nstL_2.idata, var_names=["betas", "alphas"])

/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:596: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:991: RuntimeWarning: invalid value encountered in scalar divide
  varsd = varvar / evar / 4

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
betas[ic]	-0.002	0.001	-0.004	-0.001	0.000	0.000	3940.0	2816.0	1.0
betas[oc]	-0.006	0.001	-0.009	-0.003	0.000	0.000	3871.0	2900.0	1.0
alphas[gc]	-0.154	0.724	-1.508	1.199	0.016	0.012	2176.0	2402.0	1.0
alphas[ec]	0.110	0.735	-1.259	1.497	0.016	0.012	2097.0	2306.0	1.0
alphas[gr]	-0.671	0.752	-2.023	0.815	0.016	0.013	2335.0	2327.0	1.0
alphas[er]	0.678	0.754	-0.715	2.078	0.015	0.015	2486.0	2355.0	1.0
alphas[hp]	0.000	0.000	0.000	0.000	0.000	NaN	4000.0	4000.0	NaN

Again the parameter estimates seem to be recovered sensibly on the beta coefficients, but the question remains as to whether this additional nesting structure will help support plausible counterfactual reasoning. Note how the model struggles to identify the the intercept terms and places weight on

fig, axs = plt.subplots(1, 3, figsize=(20, 6))
axs = axs.flatten()
az.plot_ppc(nstL_1.idata, ax=axs[0])
axs[0].set_title("Single Level Nesting Model")
az.plot_forest(
    [nstL_1.idata, nstL_2.idata],
    var_names=["betas"],
    combined=True,
    ax=axs[1],
    model_names=["Nested Single Level", "Nested 2 Level"],
)
axs[2].set_title("Two Level Nesting Model")
az.plot_ppc(nstL_2.idata, ax=axs[2]);

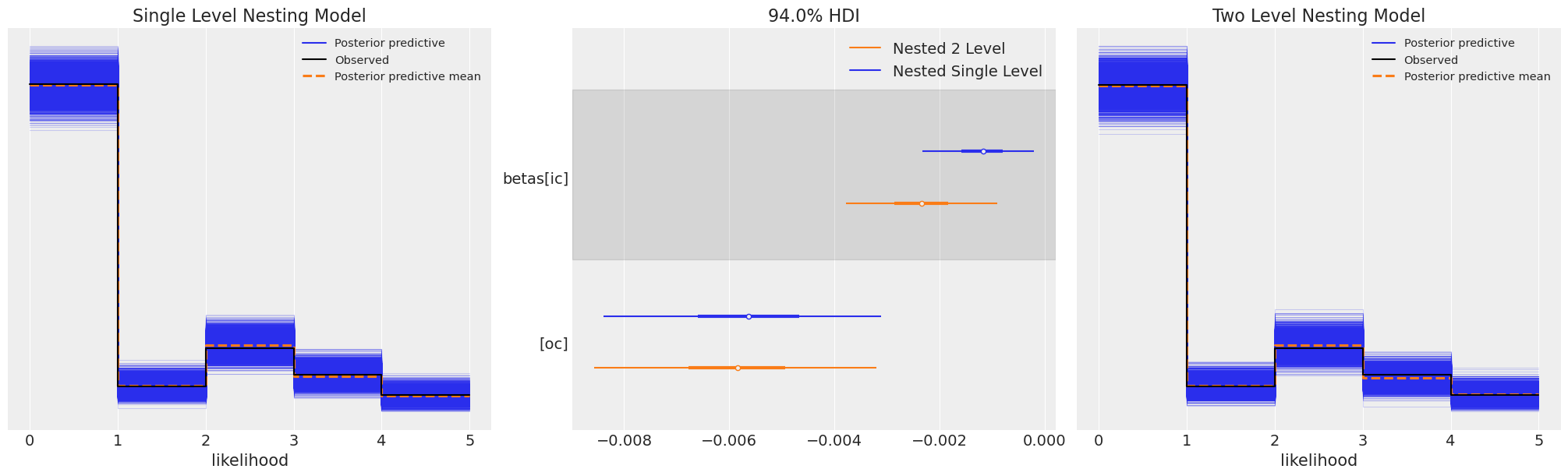
Both models seem to recover posterior predictive distributions well, but vary slightly in the estimate parameters. Let’s check the counterfactual inferences.

Making Interventions in Structured Markets

new_policy_df = df.copy()
new_policy_df[["ic_ec", "ic_er"]] = new_policy_df[["ic_ec", "ic_er"]] * 1.5

idata_new_policy_1 = nstL_1.apply_intervention(new_choice_df=new_policy_df)
idata_new_policy_2 = nstL_2.apply_intervention(new_choice_df=new_policy_df)

Sampling: [likelihood]

Sampling: [likelihood]

Here we can see that both nesting structures recover non-proportional patterns of product substitution. We have elided the IIA feature of the multinomial logit and can continue to assess whether or not the behaviour implications of these utility theory makes sense.

change_df_1 = nstL_1.calculate_share_change(nstL_1.idata, nstL_1.intervention_idata)
change_df_1

	policy_share	new_policy_share	relative_change
product
gc	0.634409	0.659635	0.039763
ec	0.072040	0.043547	-0.395510
gr	0.149110	0.182306	0.222624
er	0.090661	0.048501	-0.465027
hp	0.053779	0.066010	0.227423

change_df_2 = nstL_2.calculate_share_change(nstL_2.idata, nstL_2.intervention_idata)
change_df_2

	policy_share	new_policy_share	relative_change
product
gc	0.635015	0.676790	0.065786
ec	0.072617	0.023594	-0.675095
gr	0.148504	0.209512	0.410820
er	0.087550	0.031772	-0.637102
hp	0.056314	0.058332	0.035838

Visualising the Substitution Patterns

fig = nstL_1.plot_change(change_df=change_df_1, figsize=(10, 6))

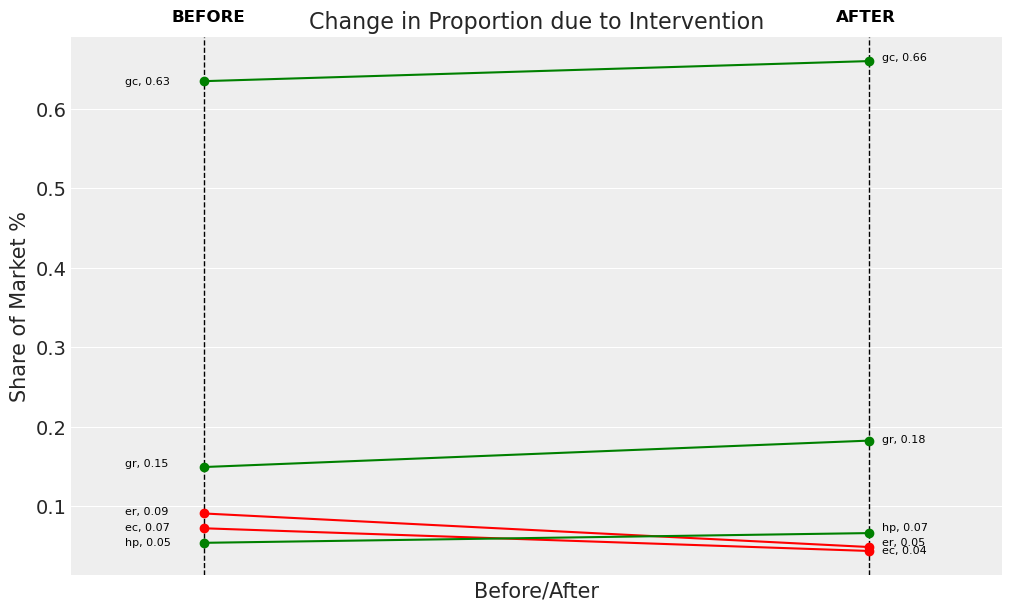
fig = nstL_2.plot_change(change_df=change_df_2, figsize=(10, 6))

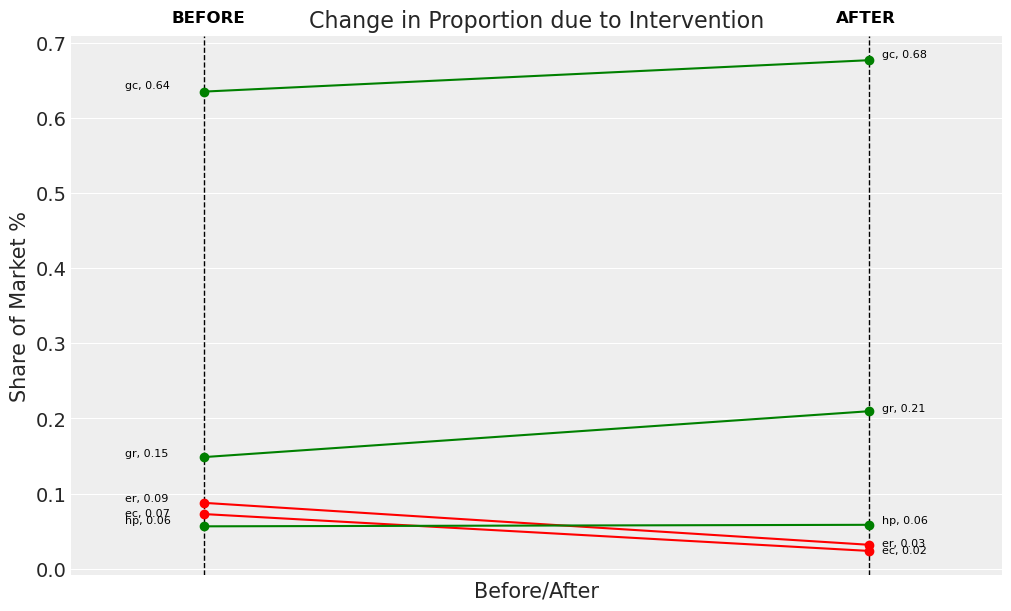
A Different Market

Let’s now briefly look at a different market that highlights a limitation of the nested logit model.

data_path = data_dir / "choice_crackers.csv"
df_new = pd.read_csv(data_path)
last_chosen = pd.get_dummies(df_new["lastChoice"]).drop("private", axis=1).astype(int)
last_chosen.columns = [col + "_last_chosen" for col in last_chosen.columns]
df_new[last_chosen.columns] = last_chosen
df_new

	personId	disp_sunshine	disp_keebler	disp_nabisco	disp_private	feat_sunshine	feat_keebler	feat_nabisco	feat_private	price_sunshine	price_keebler	price_nabisco	price_private	choice	lastChoice	personChoiceId	choiceId	keebler_last_chosen	nabisco_last_chosen	sunshine_last_chosen
0	1	0	0	0	0	0	0	0	0	0.99	1.09	0.99	0.71	nabisco	nabisco	1	1	0	1	0
1	1	1	0	0	0	0	0	0	0	0.49	1.09	1.09	0.78	sunshine	nabisco	2	2	0	1	0
2	1	0	0	0	0	0	0	0	0	1.03	1.09	0.89	0.78	nabisco	sunshine	3	3	0	0	1
3	1	0	0	0	0	0	0	0	0	1.09	1.09	1.19	0.64	nabisco	nabisco	4	4	0	1	0
4	1	0	0	0	0	0	0	0	0	0.89	1.09	1.19	0.84	nabisco	nabisco	5	5	0	1	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
3151	136	0	0	0	0	0	0	0	0	1.09	1.19	0.99	0.55	private	private	9	3152	0	0	0
3152	136	0	0	0	1	0	0	0	0	0.78	1.35	1.04	0.65	private	private	10	3153	0	0	0
3153	136	0	0	0	0	0	0	0	0	1.09	1.17	1.29	0.59	private	private	11	3154	0	0	0
3154	136	0	0	0	0	0	0	0	0	1.09	1.22	1.29	0.59	private	private	12	3155	0	0	0
3155	136	0	0	0	0	0	0	0	0	1.29	1.04	1.23	0.59	private	private	13	3156	0	0	0

3156 rows × 20 columns

utility_formulas = [
    "sunshine ~ disp_sunshine + feat_sunshine + price_sunshine ",
    "keebler ~ disp_keebler + feat_keebler + price_keebler  ",
    "nabisco ~ disp_nabisco + feat_nabisco + price_nabisco  ",
    "private ~ disp_private + feat_private + price_private  ",
]


nesting_structure = {
    "private": ["private"],
    "brand": ["keebler", "sunshine", "nabisco"],
}


nstL_3 = NestedLogit(
    choice_df=df_new,
    utility_equations=utility_formulas,
    depvar="choice",
    covariates=["disp", "feat", "price"],
    nesting_structure=nesting_structure,
    model_config={
        "alphas_": Prior("Normal", mu=0, sigma=5, dims="alts"),
        "betas": Prior("Normal", mu=0, sigma=1, dims="alt_covariates"),
        "betas_fixed_": Prior("Normal", mu=0, sigma=1, dims="fixed_covariates"),
        "lambdas_nests": Prior("Beta", alpha=1, beta=1, dims="nests"),
    },
)
nstL_3

<pymc_marketing.customer_choice.nested_logit.NestedLogit at 0x3c67a4f70>

nstL_3.sample(
    fit_kwargs={
        "tune": 2000,
        "target_accept": 0.97,
        "nuts_sampler": "numpyro",
        "idata_kwargs": {"log_likelihood": True},
    }
)

Sampling: [alphas_, betas, lambdas_nests, likelihood]

There were 9 divergences after tuning. Increase `target_accept` or reparameterize.
Sampling: [likelihood]

<pymc_marketing.customer_choice.nested_logit.NestedLogit at 0x3c67a4f70>

az.summary(
    nstL_3.idata,
    var_names=["alphas", "betas"],
)

/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:596: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:991: RuntimeWarning: invalid value encountered in scalar divide
  varsd = varvar / evar / 4

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alphas[sunshine]	-0.600	2.891	-6.120	4.827	0.080	0.054	1325.0	1730.0	1.01
alphas[keebler]	-0.213	2.886	-5.536	5.383	0.079	0.054	1350.0	1732.0	1.01
alphas[nabisco]	0.777	2.892	-4.804	6.119	0.078	0.054	1392.0	1704.0	1.01
alphas[private]	0.000	0.000	0.000	0.000	0.000	NaN	4000.0	4000.0	NaN
betas[disp]	0.014	0.049	-0.072	0.112	0.001	0.001	2315.0	1693.0	1.00
betas[feat]	0.115	0.087	-0.038	0.283	0.002	0.002	1852.0	1479.0	1.00
betas[price]	-2.317	0.665	-3.541	-1.079	0.023	0.013	809.0	1311.0	1.00

ax = az.plot_forest(
    nstL_3.idata,
    var_names=["alphas", "betas"],
    combined=True,
    r_hat=True,
)
ax[0].axvline(0, color="k", linestyle="--")
ax[0].set_title("Parameter Estimates from the Nested Logit Model");

/Users/nathanielforde/mambaforge/envs/pymc-marketing-dev/lib/python3.10/site-packages/arviz/stats/diagnostics.py:596: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)

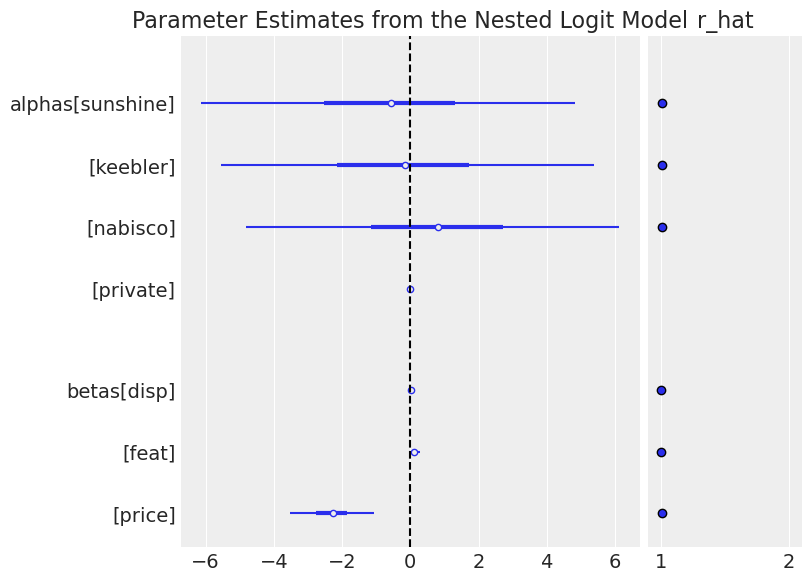
This model suggests plausibly that price increases have a strongly negative effect of the purchase probability of crackers. However, we should note that we’re ignoring information when we use the nested logit in this context. The data set records multiple purchasing decisions for each individual and by failing to model this fact we lose insight into individual heterogeneity in their responses to price shifts. To gain more insight into this aspect of the purchasing decisions of individuals we might augment our model with hierarchical components or switch to alternative Mixed logit model.

Choosing a Market Structure

Causal inference is hard and predicting the counterfactual actions of agents in a competitive market is very hard. There is no guarantee that a nested logit model will accurately represent the choice of any particular agent, but you can be hopeful that it highlights expected patterns of choice when the nesting structure reflects the natural segmentation of a market. Nests should group alternatives that share unobserved similarities, ideally driven by a transparent theory of the market structure. Well-specified nests should show stronger substitution within nests than across nests, and you can inspect the substitution patterns as above. Ideally you can always try and hold out some test data to evaluate the implications of your fitted model. Discrete choice models are causal inference models and their structural specification should support generalisable inference across future and counterfactual situations.

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Fri Jun 20 2025

Python implementation: CPython
Python version       : 3.10.17
IPython version      : 8.35.0

pytensor: 2.31.3

matplotlib    : 3.10.1
pandas        : 2.2.3
arviz         : 0.21.0
pymc_marketing: 0.14.0

Watermark: 2.5.0