Introduction to the Bass Diffusion Model

What is the Bass Model?

The Bass diffusion model, developed by Frank Bass in 1969, is a mathematical model that describes how new products get adopted in a population over time. It’s widely used in marketing to forecast sales of new products, especially when historical data is limited or non-existent.

The model captures the entire lifecycle of product adoption, from introduction to saturation, making it a powerful tool for product planning and marketing strategy development.

The Motivation Behind the Bass Model

Before the Bass model, companies struggled to predict the adoption patterns of new products. Traditional forecasting methods often failed because they couldn’t account for the social dynamics that drive product adoption. Frank Bass recognized that product adoption follows a distinct pattern:

• Initial slow growth: When a product first launches, adoption starts slowly

• Rapid acceleration: As more people adopt, word-of-mouth spreads and adoption accelerates

• Eventual saturation: Eventually, the market becomes saturated and adoption slows down

The Bass model provides a mathematical framework to capture these patterns, enabling businesses to make more informed decisions about production planning, inventory management, and marketing resource allocation.

Mathematical Formulation

The Bass model is based on a differential equation that describes the rate of adoption:

\[\frac{f(t)}{1-F(t)} = p + q F(t)\]

Where:

• \(F(t)\) is the installed base fraction (cumulative proportion of adopters)

• \(f(t)\) is the rate of change of the installed base fraction (\(f(t) = F'(t)\))

• \(p\) is the coefficient of innovation or external influence

• \(q\) is the coefficient of imitation or internal influence

The solution to this equation gives the adoption curve:

\[F(t) = \frac{1 - e^{-(p+q)t}}{1 + (\frac{q}{p})e^{-(p+q)t}}\]

The adoption rate at time \(t\) is given by:

\[f(t) = (p + q F(t))(1 - F(t))\]

Alternatively, this can be written as:

\[f(t) = \frac{(p+q)^2 \cdot e^{-(p+q)t}}{p \cdot (1+\frac{q}{p}e^{-(p+q)t})^2}\]

Key Components of the Bass Model Implementation

The Bass model implementation in PyMC-Marketing consists of several key components:

1. Adopters - The number of new adoptions at time \(t\):

\[\text{adopters}(t) = m \cdot f(p, q, t)\]

2. Innovators - Adoptions driven by external influence (advertising, etc.):

\[\text{innovators}(t) = m \cdot p \cdot (1 - F(p, q, t))\]

3. Imitators - Adoptions driven by internal influence (word-of-mouth):

\[\text{imitators}(t) = m \cdot q \cdot F(p, q, t) \cdot (1 - F(p, q, t))\]

4. Peak Adoption Time - When the adoption rate reaches its maximum:

\[\text{peak} = \frac{\ln(q) - \ln(p)}{p + q}\]

The total number of adopters over time is the sum of innovators and imitators, which equals \(\text{adopters}(t)\). All of these components are directly implemented in the PyMC model, allowing us to analyze each aspect of the diffusion process separately.

Understanding the Relationship Between Components

A key insight of the Bass model is how it decomposes adoption into two sources:

\[\text{adopters}(t) = \text{innovators}(t) + \text{imitators}(t)\]

At each time point:

• Innovators (\(m \cdot p \cdot (1 - F(t))\)) represents new adoptions coming from people who are influenced by external factors like advertising

• Imitators (\(m \cdot q \cdot F(t) \cdot (1 - F(t))\)) represents new adoptions coming from people who are influenced by previous adopters

As time progresses:

• Initially, innovators dominate the adoption process when few people have adopted (\(F(t)\) is small)

• Later, imitators become the primary source of new adoptions as the word-of-mouth effect grows

• Eventually, both decrease as the market approaches saturation (\(F(t)\) approaches 1)

The cumulative adoption at any time point is:

\[\text{Cumulative Adoption}(t) = m \cdot F(t)\]

This means that as \(t \to \infty\), the cumulative adoption approaches the total market potential \(m\):

\[\lim_{t \to \infty} \text{Cumulative Adoption}(t) = m\]

Therefore, the Bass model provides a complete accounting of the market:

• At each time point, new adopters are either innovators or imitators

• Over the entire product lifecycle, all potential adopters (m) eventually adopt the product

• The model tracks both the adoption rate (new adopters per time period) and the cumulative adoption (total adopters to date)

This structure enables marketers to understand not just how many people will adopt over time, but also the driving forces behind adoption at different stages of the product lifecycle.

Understanding the Key Parameters

The model has three main parameters:

• Market potential (m): Total number of eventual adopters (the ultimate market size)

• Innovation coefficient (p): Measures external influence like advertising and media - typically \(0.01-0.03\)

• Imitation coefficient (q): Measures internal influence like word-of-mouth - typically \(0.3-0.5\)

Parameter Interpretation

• A higher p value indicates stronger external influence (advertising, marketing)

• A higher q value indicates stronger internal influence (word-of-mouth, social interactions)

• The ratio q/p indicates the relative strength of internal vs. external influences

• The peak of adoption occurs at time

\[t^* = \frac{\ln(q / p)}{p + q}\]

Innovators vs. Imitators

The Bass model distinguishes between two types of adopters:

1. Innovators: People who adopt independently of others’ decisions, influenced mainly by mass media and external communications

   • Mathematically represented as: \(\text{innovators}(t) = m \cdot p \cdot (1 - F(p, q, t))\)

2. Imitators: People who adopt because of social influence and word-of-mouth from previous adopters

   • Mathematically represented as: \(\text{imitators}(t) = m \cdot q \cdot F(p, q, t) \cdot (1 - F(p, q, t))\)

Real-World Applications

The Bass model has been successfully applied to forecast the adoption of various products and technologies:

• Consumer durables: TVs, refrigerators, washing machines

• Technology products: Smartphones, computers, software

• Pharmaceutical products: New drugs and treatments

• Entertainment products: Movies, games, streaming services

• Services and subscriptions: Banking services, subscription plans

Business Value: Why the Bass Model Matters to Executives and Marketers

From a business perspective, the Bass diffusion model provides substantial competitive advantages and ROI benefits:

1. Resource Optimization and Cash Flow Management

• Production Planning: Avoid costly overproduction or stockouts by accurately forecasting demand curves

• Marketing Budget Allocation: Optimize spending across the product lifecycle, investing more during key inflection points

• Supply Chain Efficiency: Coordinate with suppliers and distributors based on predicted adoption rates

• Cash Flow Optimization: Better predict revenue streams, improving financial planning and investor relations

2. Strategic Decision Making

• Launch Timing: Determine the optimal time to enter a market based on diffusion patterns

• Pricing Strategy: Implement dynamic pricing strategies aligned with the adoption curve

• Competitive Analysis: Compare your product’s adoption parameters with competitors to identify strengths and weaknesses

• Product Portfolio Management: Make informed decisions about when to phase out older products and introduce new ones

3. Risk Mitigation

• Scenario Planning: Test different market assumptions and external factors through parameter variations

• Early Warning System: Identify deviations from expected adoption curves early, enabling faster intervention

• Investment Justification: Provide data-driven forecasts to justify R&D and marketing investments to stakeholders

4. Performance Measurement

• Marketing Effectiveness: Measure the impact of marketing campaigns on the innovation coefficient (p)

• Word-of-Mouth Strength: Quantify the power of your brand’s social influence through the imitation coefficient (q)

• Total Market Potential: Validate or adjust your total addressable market estimates (m)

In today’s data-driven business environment, companies that effectively utilize models like Bass diffusion gain a significant competitive edge through more precise forecasting, better resource allocation, and strategic market timing.

Bayesian Extensions

In this notebook, we show how to generate simulated data from the Bass model and fit a Bayesian model to it. The Bayesian formulation offers several advantages:

• Uncertainty quantification through prior distributions on parameters

• Hierarchical modeling for multiple products or markets

• Incorporation of expert knowledge through informative priors

• Full probability distributions for future adoption forecasts

What we’ll do in this notebook

In this notebook, we’ll:

1. Set up parameters for a Bass model simulation

2. Generate simulated adoption data for multiple products

3. Fit the Bass model to our simulated data using PyMC

4. Visualize the adoption curves

Prepare Notebook

from typing import Any

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import numpy.typing as npt
import pandas as pd
import pymc as pm
import xarray as xr

from pymc_marketing.bass.model import create_bass_model
from pymc_marketing.plot import plot_curve
from pymc_marketing.prior import Prior, Scaled

az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = [12, 7]
plt.rcParams["figure.dpi"] = 100

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "retina"

seed: int = sum(map(ord, "bass"))
rng: np.random.Generator = np.random.default_rng(seed=seed)

Setting Up Simulation Parameters

First, we’ll set up the parameters for our simulation. This includes:

• The time period for our simulation (in weeks)

• The number of products to simulate

• Start dates for the simulation period

def setup_simulation_parameters(
    n_weeks: int = 52,
    n_products: int = 9,
    start_date: str = "2023-01-01",
    cutoff_start_date: str = "2023-12-01",
) -> tuple[
    npt.NDArray[np.int_],
    pd.DatetimeIndex,
    pd.DatetimeIndex,
    list[str],
    pd.Series,
    dict[str, Any],
]:
    """Set up initial parameters for the Bass diffusion model simulation.

    Parameters
    ----------
    n_weeks : int
        Number of weeks to simulate
    n_products : int
        Number of products to include in the simulation
    start_date : str
        Starting date for the simulation period
    cutoff_start_date : str
        Latest possible start date for products

    Returns
    -------
    T : numpy.ndarray
        Time array (weeks)
    possible_dates : pandas.DatetimeIndex
        All dates in the simulation period
    possible_start_dates : pandas.DatetimeIndex
        Possible start dates for products
    products : list
        List of product names
    product_start : pandas.Series
        Start date for each product
    coords : dict
        Coordinates for PyMC model
    """
    # Set a seed for reproducibility
    seed = sum(map(ord, "bass"))
    rng = np.random.default_rng(seed)

    # Create time array and date range
    T = np.arange(n_weeks)
    possible_dates = pd.date_range(start_date, freq="W-MON", periods=n_weeks)
    cutoff_start_date = pd.to_datetime(cutoff_start_date)
    cutoff_start_date = cutoff_start_date + pd.DateOffset(weeks=1)
    possible_start_dates = possible_dates[possible_dates < cutoff_start_date]

    # Generate product names and random start dates
    products = [f"P{i}" for i in range(n_products)]
    product_start = pd.Series(
        rng.choice(possible_start_dates, size=len(products)),
        index=pd.Index(products, name="product"),
    )

    coords = {"T": T, "product": products}
    return T, possible_dates, possible_start_dates, products, product_start, coords

Creating Prior Distributions

For our Bayesian Bass model, we need to specify prior distributions for the key parameters:

• m (market potential): How many units can potentially be sold in total

• p (innovation coefficient): Rate of adoption from external influences

• q (imitation coefficient): Rate of adoption from internal/social influences

• likelihood: The probability distribution that models the observed adoption data

For the market potential m we use a scaling trick to specify a scale-free prior and then add a global factor:

def create_bass_priors(factor: float) -> dict[str, Prior | Scaled]:
    """Define prior distributions for the Bass model parameters.

    Returns
    -------
    dict
        Dictionary of prior distributions for m, p, q, and likelihood

    Notes
    -----
    - m: Market potential (scaled Gamma distribution)
    - p: Innovation coefficient (Beta distribution)
    - q: Imitation coefficient (Beta distribution)
    - likelihood: Observation model (Negative Binomial)
    """
    return {
        # We use a scaled Gamma distribution for the market potential.
        "m": Scaled(Prior("Gamma", mu=1, sigma=0.1, dims="product"), factor=factor),
        "p": Prior("Beta", mu=0.03, dims="product").constrain(lower=0.01, upper=0.03),
        "q": Prior("Beta", dims="product").constrain(lower=0.3, upper=0.5),
        "likelihood": Prior("NegativeBinomial", n=1.5, dims="product"),
    }

Let’s generate and visualize the priors.

FACTOR = 50_000
priors = create_bass_priors(factor=FACTOR)

/Users/will/mamba/envs/pymc-marketing-dev/lib/python3.10/site-packages/preliz/distributions/beta.py:127: RuntimeWarning: invalid value encountered in scalar divide
  mu = alpha / alpha_plus_beta
/Users/will/mamba/envs/pymc-marketing-dev/lib/python3.10/site-packages/preliz/distributions/beta.py:128: RuntimeWarning: invalid value encountered in scalar divide
  sigma = (alpha * beta) ** 0.5 / alpha_plus_beta / (alpha_plus_beta + 1) ** 0.5
 The requested mass is 0.95, but the computed one is 0.528

fig, ax = plt.subplots(nrows=2, ncols=1, figsize=(15, 12))

priors["p"].preliz.plot_pdf(ax=ax[0])
ax[0].set(title="Innovation Coefficient (p)")
priors["q"].preliz.plot_pdf(ax=ax[1])
ax[1].set(title="Imitation Coefficient (q)")
fig.suptitle(
    "Prior Distributions for Bass Model Parameters",
    fontsize=18,
    fontweight="bold",
    y=0.95,
);

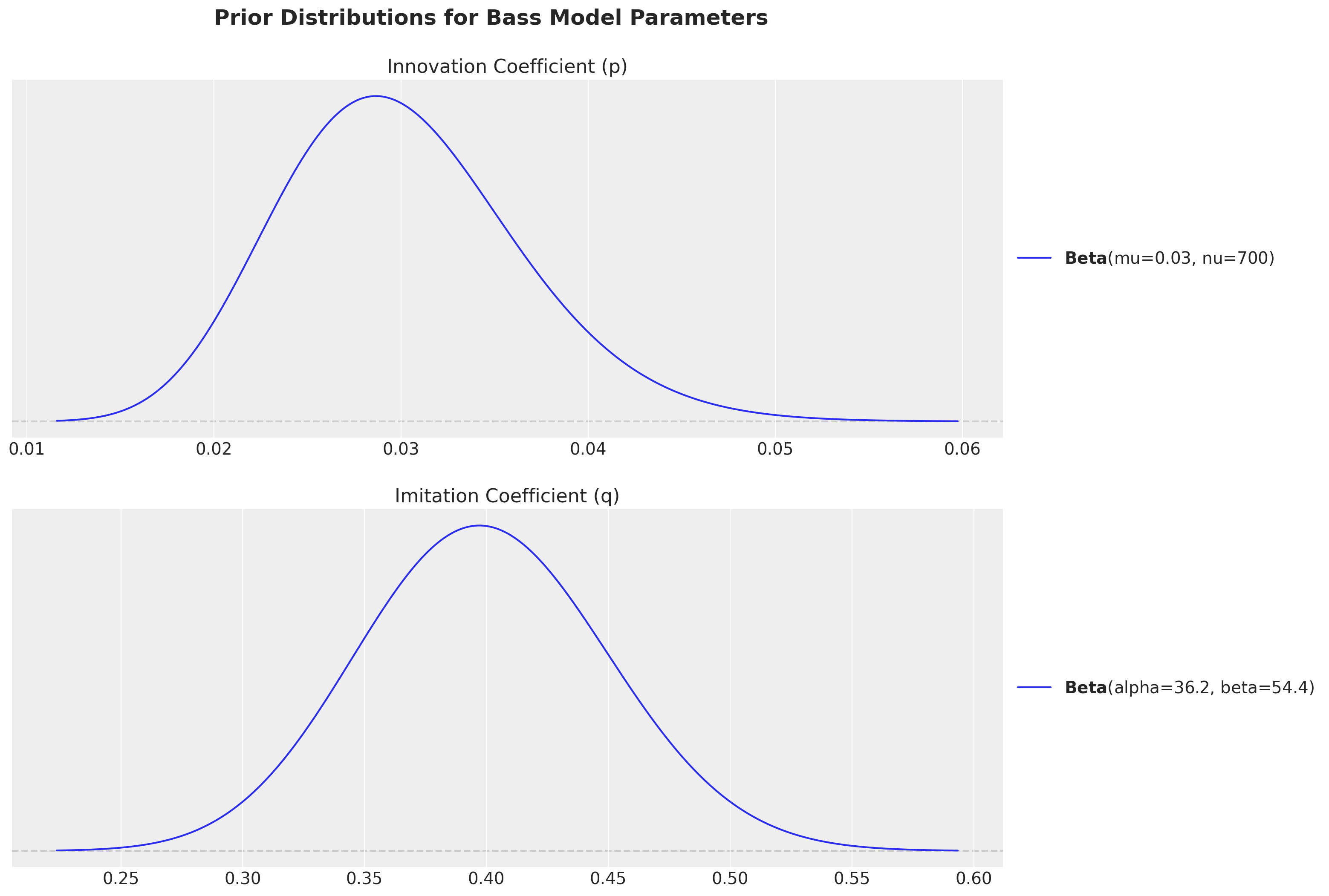
Observe we have chosen the priors within the usual ranges of empirical studies:

• Innovation coefficient (p): Measures external influence like advertising and media - typically \(0.01-0.03\)

• Imitation coefficient (q): Measures internal influence like word-of-mouth - typically \(0.3-0.5\)

Generate Synthetic Data

With the generative Bass model, we can generate a synthetic dataset by sampling from the prior and choosing one particular sample to use as observed data. For this purpose we define two auxiliary functions.

def sample_prior_bass_data(model: pm.Model) -> xr.DataArray:
    """Generate a sample from the prior predictive distribution of the Bass model.

    Parameters
    ----------
    model : pymc.Model
        The PyMC model to sample from

    Returns
    -------
    xarray.DataArray
        Simulated adoption data
    """
    with model:
        idata = pm.sample_prior_predictive(random_seed=rng)
    return idata["prior"]["y"].sel(chain=0, draw=0)


def transform_to_actual_dates(bass_data, product_start, possible_dates) -> pd.DataFrame:
    """Transform simulation data from time index to calendar dates.

    Parameters
    ----------
    bass_data : xarray.DataArray
        Simulated bass model data
    product_start : pandas.Series
        Start date for each product
    possible_dates : pandas.DatetimeIndex
        All dates in the simulation period

    Returns
    -------
    pandas.DataFrame
        Adoption data with actual calendar dates
    """
    bass_data = bass_data.to_dataset()
    bass_data["product_start"] = product_start.to_xarray()

    df_bass_data = (
        bass_data.to_dataframe().drop(columns=["chain", "draw"]).reset_index()
    )
    df_bass_data["actual_date"] = df_bass_data["product_start"] + pd.to_timedelta(
        7 * df_bass_data["T"], unit="days"
    )

    return (
        df_bass_data.set_index(["actual_date", "product"])
        .y.unstack(fill_value=0)
        .reindex(possible_dates, fill_value=0)
    )

Now we can generate the observed data:

# Setup simulation parameters
T, possible_dates, _, products, product_start, coords = setup_simulation_parameters()

# Create and configure the Bass model
generative_model = create_bass_model(t=T, coords=coords, observed=None, priors=priors)

# Sample and select one "observed" dataset.
bass_data = sample_prior_bass_data(generative_model)
actual_data = transform_to_actual_dates(bass_data, product_start, possible_dates)

Sampling: [m_unscaled, p, q, y]

The actual_data data frame has the typical format of a real dataset.

actual_data

product	P0	P1	P2	P3	P4	P5	P6	P7	P8
2023-01-02	0	0	451	0	0	0	0	0	0
2023-01-09	0	0	56	0	0	0	0	0	0
2023-01-16	0	0	1948	0	0	0	0	0	0
2023-01-23	0	0	3742	0	0	0	0	0	0
2023-01-30	0	239	156	0	0	137	0	0	0
2023-02-06	0	4199	4732	0	0	2208	0	0	0
2023-02-13	0	1646	6477	0	0	1671	0	0	0
2023-02-20	0	1810	2824	0	0	780	0	0	0
2023-02-27	0	17004	2583	1485	0	6002	0	0	0
2023-03-06	0	4956	2508	2679	0	8211	0	0	0
2023-03-13	1277	7956	3255	2340	0	2404	0	0	0
2023-03-20	1403	4926	1030	3838	0	3646	0	0	0
2023-03-27	1818	1091	3145	1443	0	13557	0	0	0
2023-04-03	2865	4696	613	85	0	2857	0	0	0
2023-04-10	1410	8236	717	2858	0	3112	0	0	0
2023-04-17	1472	499	77	3519	0	3920	0	0	0
2023-04-24	11868	1783	340	2431	0	1661	0	0	0
2023-05-01	4669	102	314	8487	0	2908	0	0	0
2023-05-08	3423	61	210	1479	0	2729	0	0	0
2023-05-15	3625	1226	11	1544	0	2125	0	0	0
2023-05-22	1591	256	110	391	0	1164	0	0	0
2023-05-29	3351	149	78	2397	0	849	0	0	0
2023-06-05	1246	205	9	205	0	1060	0	0	0
2023-06-12	1805	106	22	187	0	229	0	0	0
2023-06-19	1353	75	15	131	0	38	0	0	0
2023-06-26	457	48	5	116	0	88	0	0	0
2023-07-03	170	46	8	108	0	79	0	0	0
2023-07-10	44	67	6	57	0	16	0	0	0
2023-07-17	271	8	1	37	0	14	0	0	0
2023-07-24	42	0	1	4	0	19	0	0	2578
2023-07-31	32	6	1	9	0	0	0	0	1418
2023-08-07	93	5	0	3	0	10	0	0	1005
2023-08-14	83	1	1	0	0	4	0	0	2560
2023-08-21	47	0	0	3	0	1	0	0	3666
2023-08-28	8	0	0	1	0	0	0	0	13816
2023-09-04	4	0	0	0	0	0	0	2496	7358
2023-09-11	4	0	0	0	0	0	556	1266	6785
2023-09-18	2	0	0	0	0	3	2151	3637	2370
2023-09-25	2	0	0	0	0	0	4980	1431	1351
2023-10-02	0	1	0	1	0	0	2124	507	2038
2023-10-09	0	0	0	0	0	0	14239	1632	3441
2023-10-16	0	0	0	0	0	0	25224	4681	562
2023-10-23	0	0	0	0	0	0	17233	2095	3801
2023-10-30	0	0	0	0	1042	0	4728	1408	446
2023-11-06	0	0	0	0	1776	0	1890	1890	487
2023-11-13	0	0	0	0	1697	0	1058	3665	673
2023-11-20	0	0	0	0	6648	0	943	391	169
2023-11-27	0	0	0	0	4746	0	605	2720	374
2023-12-04	0	0	0	0	1843	0	1554	1382	98
2023-12-11	0	0	0	0	3598	0	2304	147	151
2023-12-18	0	0	0	0	6576	0	124	2582	42
2023-12-25	0	0	0	0	3610	0	215	110	160

On the other hand, the bass_data has the same data as arrays indexed by time (relative) and product.

Let’s visualize both.

fig, ax = plt.subplots(
    nrows=2, ncols=1, figsize=(15, 12), sharex=False, sharey=True, layout="constrained"
)

# Plot raw simulated data (by time step)
bass_data.to_series().unstack().plot(ax=ax[0])
ax[0].legend(
    title="Product", title_fontsize=14, loc="center left", bbox_to_anchor=(1, 0.5)
)
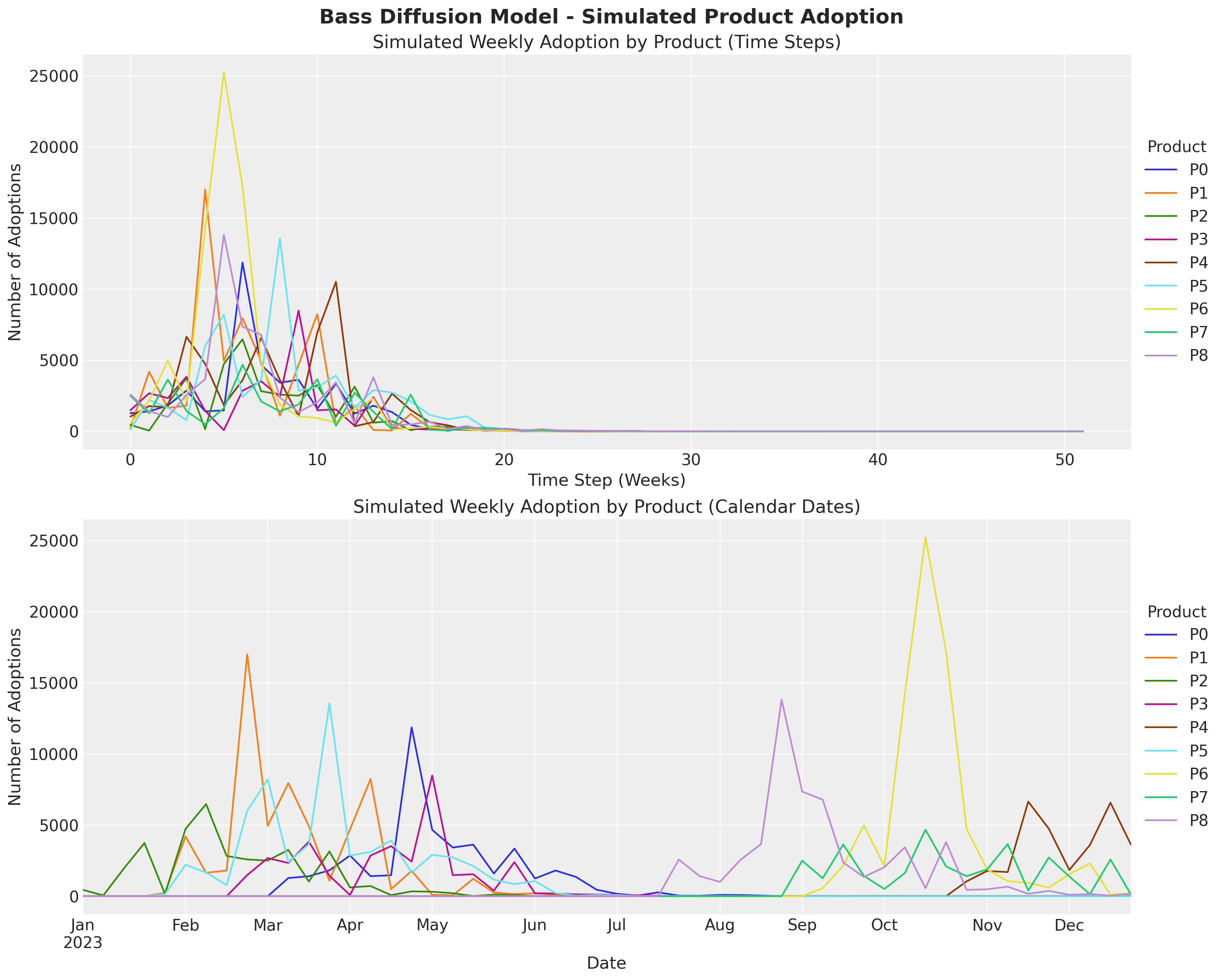
ax[0].set(
    title="Simulated Weekly Adoption by Product (Time Steps)",
    xlabel="Time Step (Weeks)",
    ylabel="Number of Adoptions",
)

# Plot data with actual calendar dates
actual_data.plot(ax=ax[1])
ax[1].legend(
    title="Product", title_fontsize=14, loc="center left", bbox_to_anchor=(1, 0.5)
)
ax[1].set(
    title="Simulated Weekly Adoption by Product (Calendar Dates)",
    xlabel="Date",
    ylabel="Number of Adoptions",
)

fig.suptitle(
    "Bass Diffusion Model - Simulated Product Adoption", fontsize=18, fontweight="bold"
);

Fit the Model

We are now ready to fit the model and generate the posterior predictive distributions.

# We condition the model on observed data.
with pm.observe(generative_model, {"y": bass_data.values}) as model:
    idata = pm.sample(
        tune=1_500,
        draws=2_000,
        chains=4,
        nuts_sampler="nutpie",
        compile_kwargs={"mode": "NUMBA"},
        random_seed=rng,
    )

    idata.extend(
        pm.sample_posterior_predictive(
            idata, model=model, extend_inferencedata=True, random_seed=rng
        )
    )

Sampling ... ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 100% 0:00:00 / 0:00:01

We do not have any divergences. Let’s look at the summary of the parameters.

az.summary(data=idata, var_names=["p", "q", "m"])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
p[P0]	0.026	0.005	0.018	0.036	0.000	0.000	10750.0	5899.0	1.0
p[P1]	0.030	0.005	0.020	0.039	0.000	0.000	11579.0	6089.0	1.0
p[P2]	0.027	0.005	0.017	0.036	0.000	0.000	11292.0	5970.0	1.0
p[P3]	0.030	0.005	0.020	0.040	0.000	0.000	12126.0	6250.0	1.0
p[P4]	0.026	0.005	0.018	0.035	0.000	0.000	12027.0	6287.0	1.0
p[P5]	0.021	0.004	0.013	0.028	0.000	0.000	10939.0	5817.0	1.0
p[P6]	0.032	0.005	0.022	0.042	0.000	0.000	11071.0	5834.0	1.0
p[P7]	0.030	0.005	0.020	0.039	0.000	0.000	12427.0	5130.0	1.0
p[P8]	0.030	0.005	0.021	0.040	0.000	0.000	11252.0	6353.0	1.0
q[P0]	0.402	0.019	0.368	0.439	0.000	0.000	10124.0	5923.0	1.0
q[P1]	0.394	0.019	0.360	0.429	0.000	0.000	10431.0	6172.0	1.0
q[P2]	0.397	0.019	0.363	0.434	0.000	0.000	11818.0	6179.0	1.0
q[P3]	0.450	0.022	0.413	0.493	0.000	0.000	12285.0	6374.0	1.0
q[P4]	0.354	0.017	0.324	0.386	0.000	0.000	11480.0	6068.0	1.0
q[P5]	0.385	0.018	0.350	0.418	0.000	0.000	9830.0	5566.0	1.0
q[P6]	0.430	0.020	0.393	0.468	0.000	0.000	12521.0	6256.0	1.0
q[P7]	0.344	0.017	0.311	0.375	0.000	0.000	12231.0	5460.0	1.0
q[P8]	0.339	0.017	0.307	0.369	0.000	0.000	10948.0	6146.0	1.0
m[P0]	49568.996	4491.414	40760.951	57490.821	41.520	55.743	11720.0	5933.0	1.0
m[P1]	51816.841	4487.349	43766.599	60653.332	41.988	55.334	11242.0	5793.0	1.0
m[P2]	47118.829	4436.392	39310.947	55843.304	41.551	54.987	11186.0	5118.0	1.0
m[P3]	48429.471	4518.438	40231.737	57157.439	41.948	54.340	11472.0	5854.0	1.0
m[P4]	51994.167	4501.491	43959.011	60680.809	43.404	54.416	10713.0	5973.0	1.0
m[P5]	53276.493	4568.591	45196.257	62426.608	46.587	61.073	9433.0	5492.0	1.0
m[P6]	53087.905	4612.168	44525.164	61948.611	45.914	58.424	10125.0	5873.0	1.0
m[P7]	47684.913	4315.345	39879.468	55899.426	40.015	50.408	11727.0	6210.0	1.0
m[P8]	51232.596	4464.032	42849.916	59268.568	43.671	57.224	10498.0	5213.0	1.0

_ = az.plot_trace(
    data=idata,
    var_names=["p", "q", "m"],
    compact=True,
    backend_kwargs={"figsize": (12, 7), "layout": "constrained"},
)
plt.gcf().suptitle("Model Trace", fontsize=16);

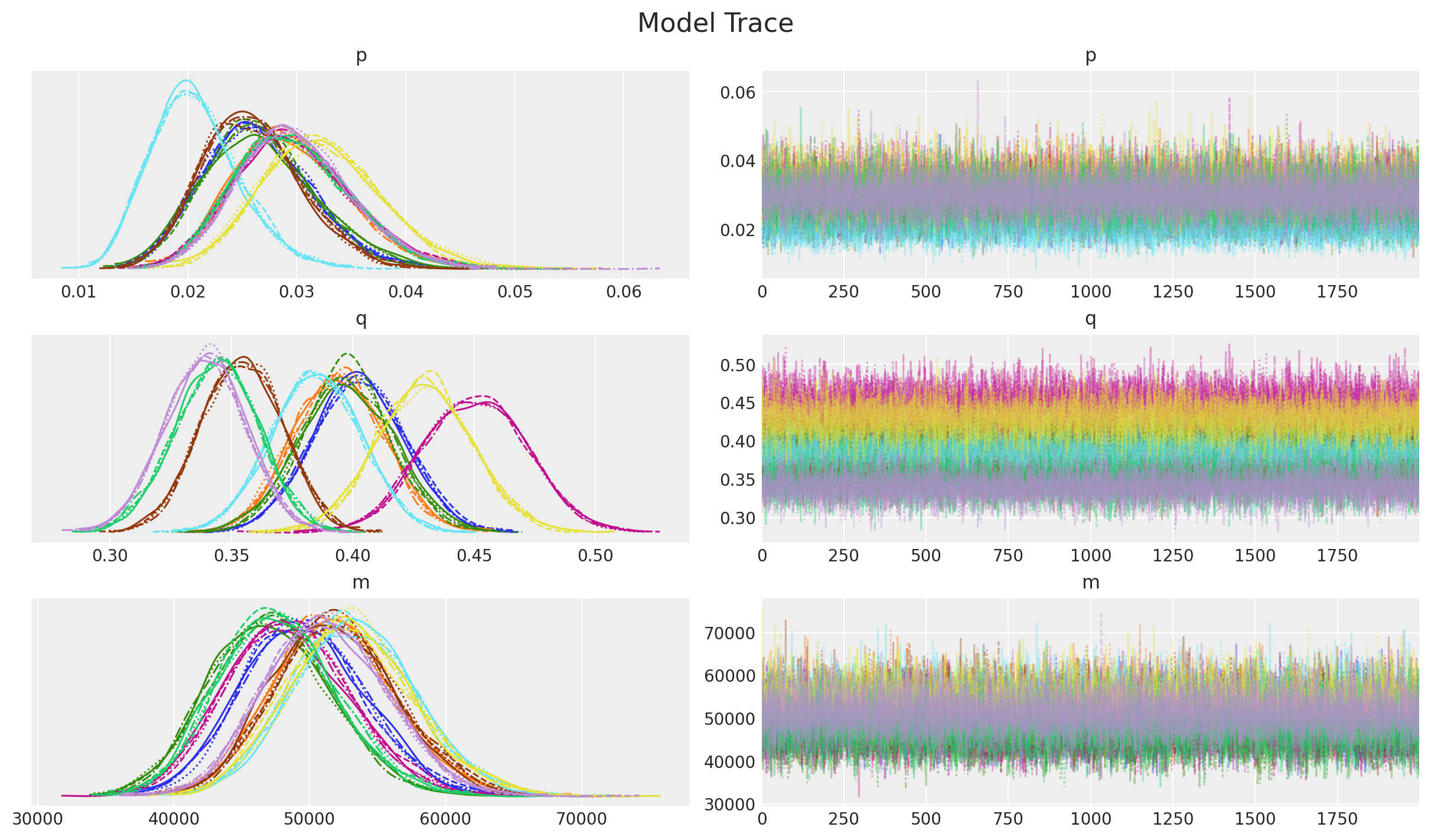
Overall, the diagnostics and trace look good.

Next, we look into the posterior distributions of the parameters.

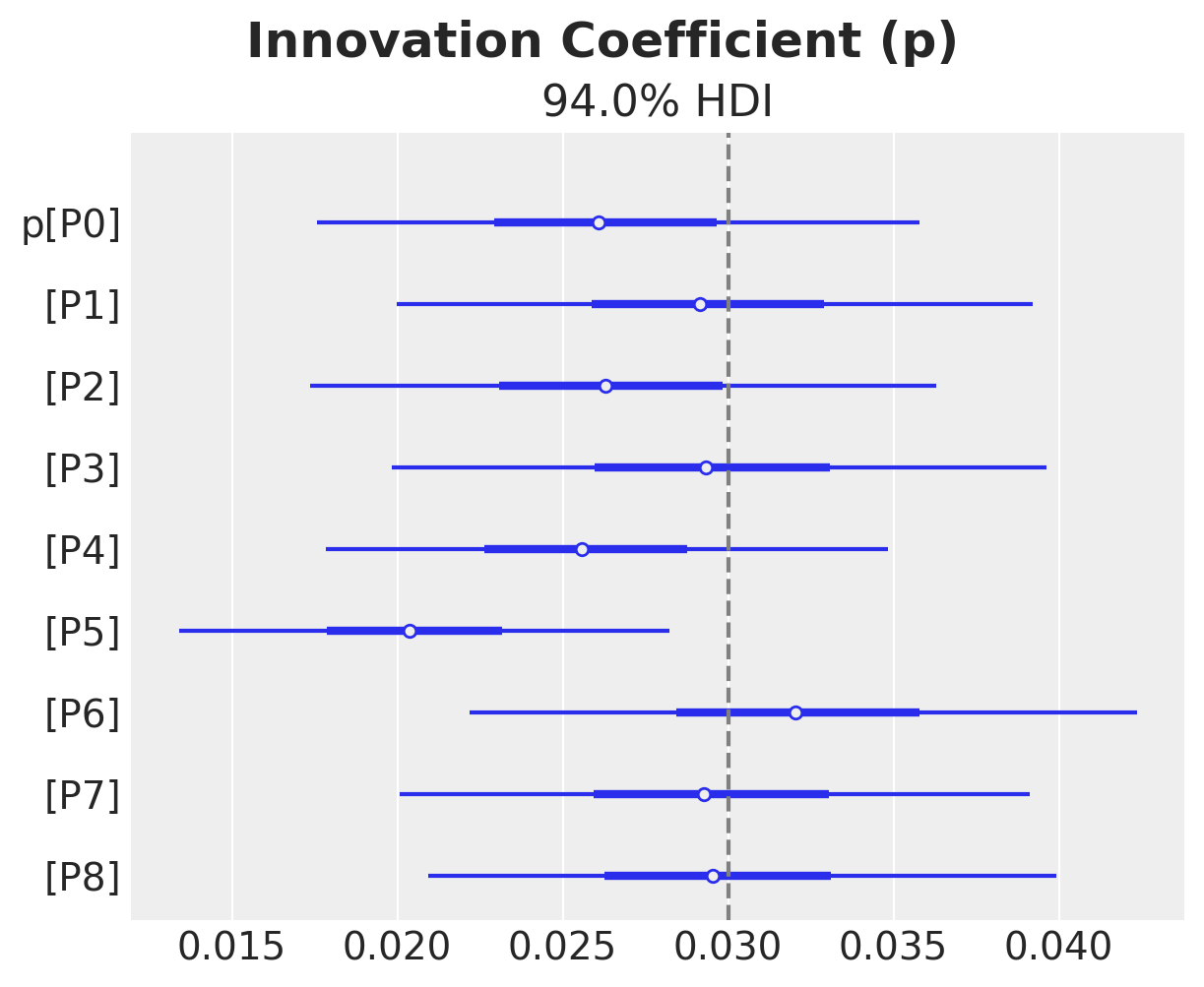
ax, *_ = az.plot_forest(idata["posterior"]["p"], combined=True)
ax.axvline(x=priors["p"].parameters["mu"], color="gray", linestyle="--")
ax.get_figure().suptitle("Innovation Coefficient (p)", fontsize=18, fontweight="bold")

Text(0.5, 0.98, 'Innovation Coefficient (p)')

ax, *_ = az.plot_forest(idata["posterior"]["q"], combined=True)
ax.axvline(x=priors["q"].preliz.mean(), color="gray", linestyle="--")
ax.get_figure().suptitle("Imitation Coefficient (q)", fontsize=18, fontweight="bold")

Text(0.5, 0.98, 'Imitation Coefficient (q)')

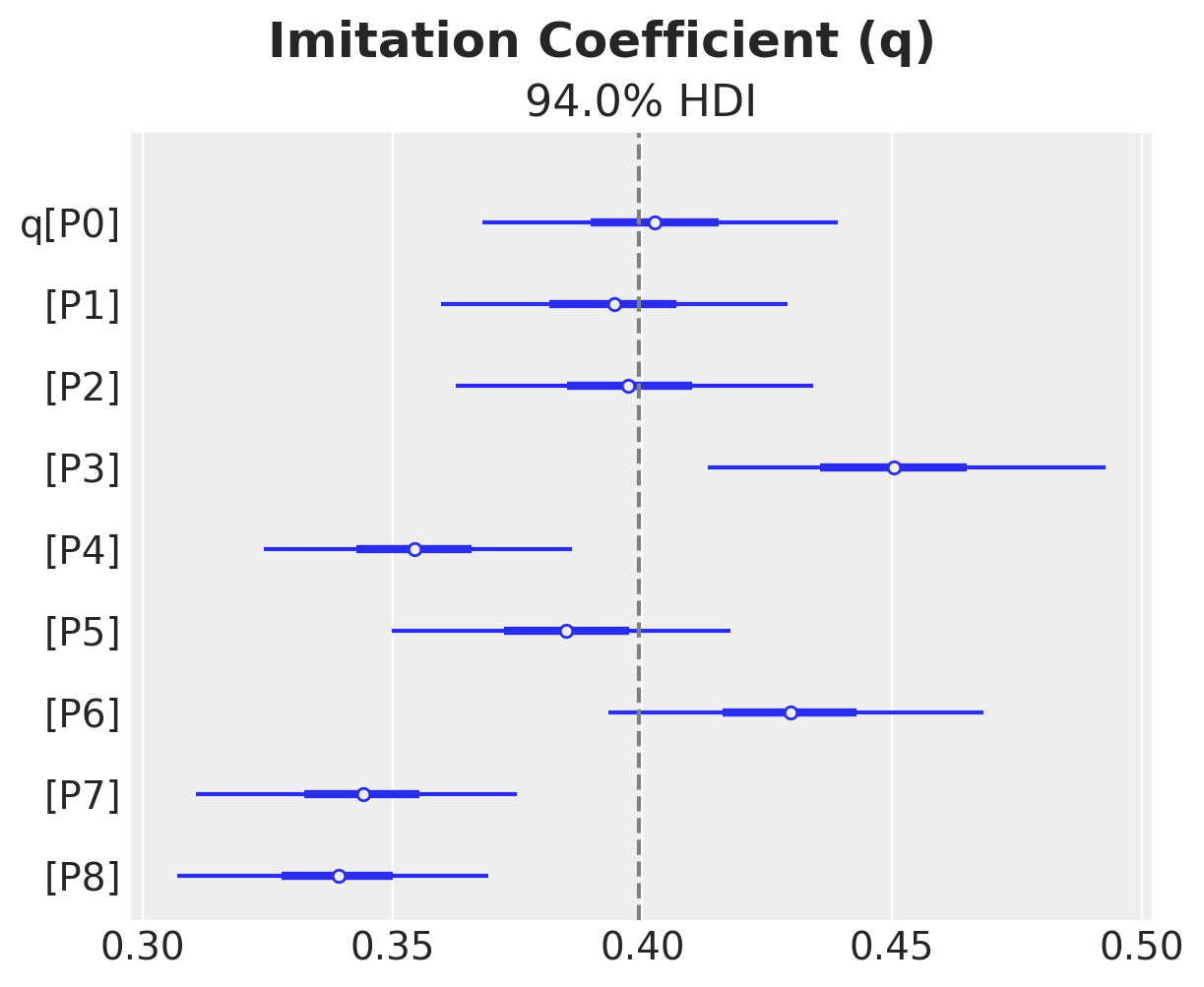
We do see some heterogeneity in the parameters, but overall they are centered around the true values (from the generative model).

Examining Posterior Predictions for Specific Products

Let’s look at the posterior predictive distributions to see how well our model captures the simulated data.

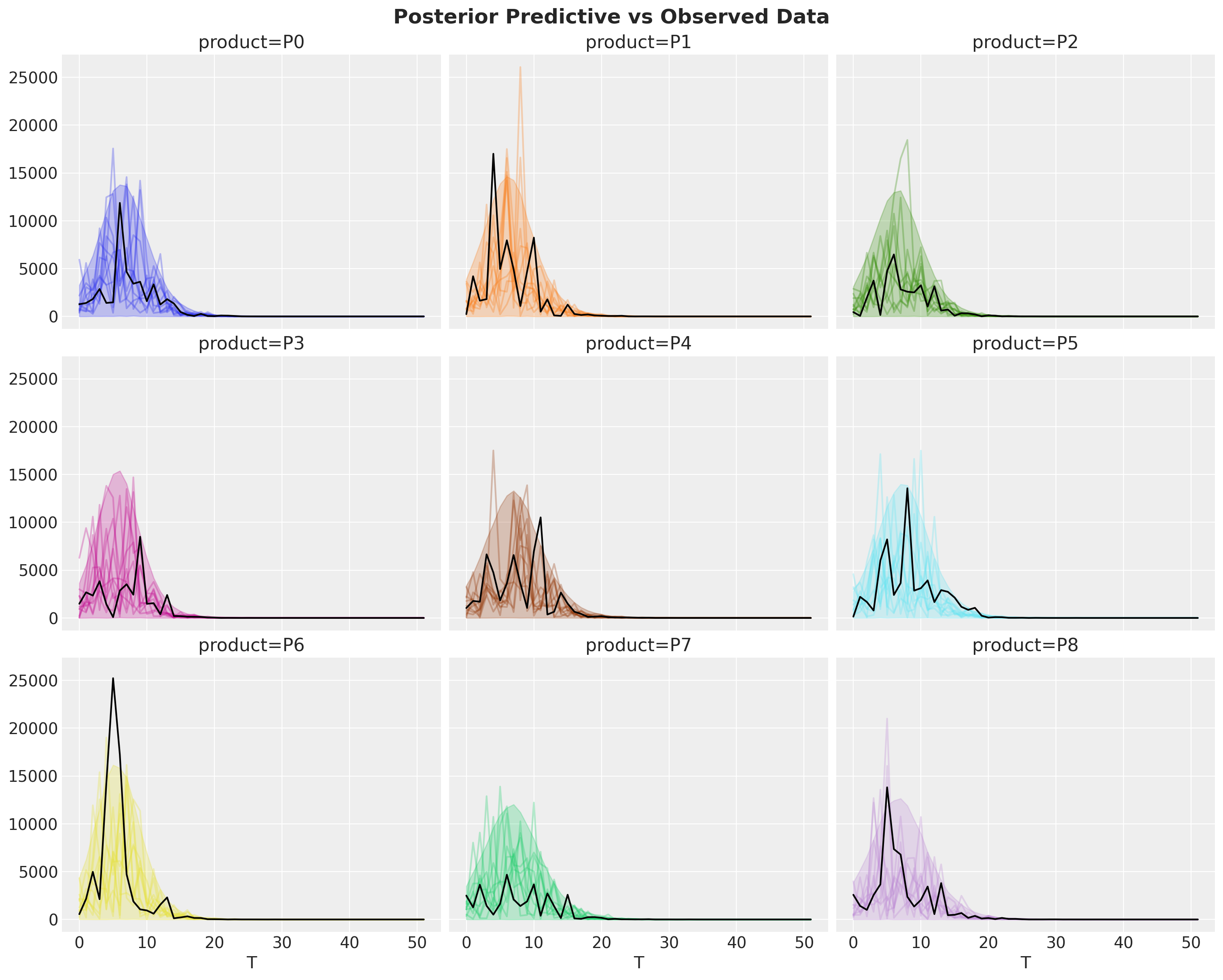
fig, axes = plt.subplots(
    nrows=3, ncols=3, figsize=(15, 12), sharex=True, sharey=True, layout="constrained"
)

idata["posterior_predictive"]["y"].pipe(plot_curve, {"T"}, axes=axes)

for i, ax in enumerate(axes.flatten()):
    ax.plot(T, bass_data[:, i], color="black")

fig.suptitle("Posterior Predictive vs Observed Data", fontsize=18, fontweight="bold");

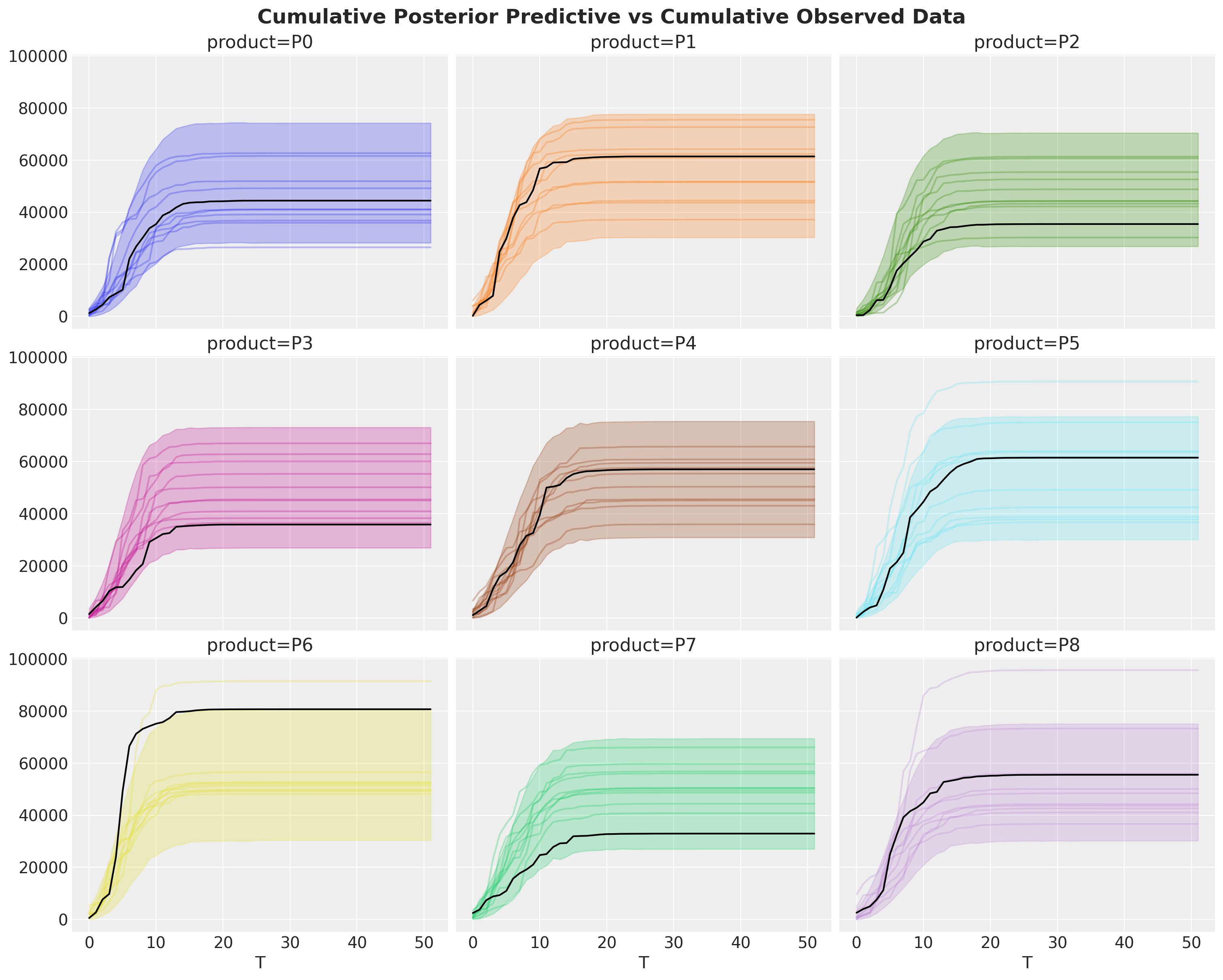
fig, axes = plt.subplots(
    nrows=3, ncols=3, figsize=(15, 12), sharex=True, sharey=True, layout="constrained"
)

idata["posterior_predictive"]["y"].cumsum(dim="T").pipe(plot_curve, {"T"}, axes=axes)

for i, ax in enumerate(axes.flatten()):
    ax.plot(T, bass_data[:, i].cumsum(), color="black")

fig.suptitle(
    "Cumulative Posterior Predictive vs Cumulative Observed Data",
    fontsize=18,
    fontweight="bold",
);

observed_cumulative = bass_data.cumsum(dim="T").isel(T=-1).to_series()

ref_val = {
    "m": [
        {"product": name, "ref_val": value}
        for name, value in observed_cumulative.items()
    ]
}

az.plot_posterior(
    idata.posterior,
    var_names=["m"],
    backend_kwargs=dict(sharex=True, layout="constrained", figsize=(15, 12)),
    ref_val=ref_val,
)

max_T = bass_data.coords["T"].max().item()
fig = plt.gcf()
fig.suptitle(
    f"Estimated Market Cap (m) vs Observed Cumulative at T={max_T}",
    fontsize=18,
    fontweight="bold",
);

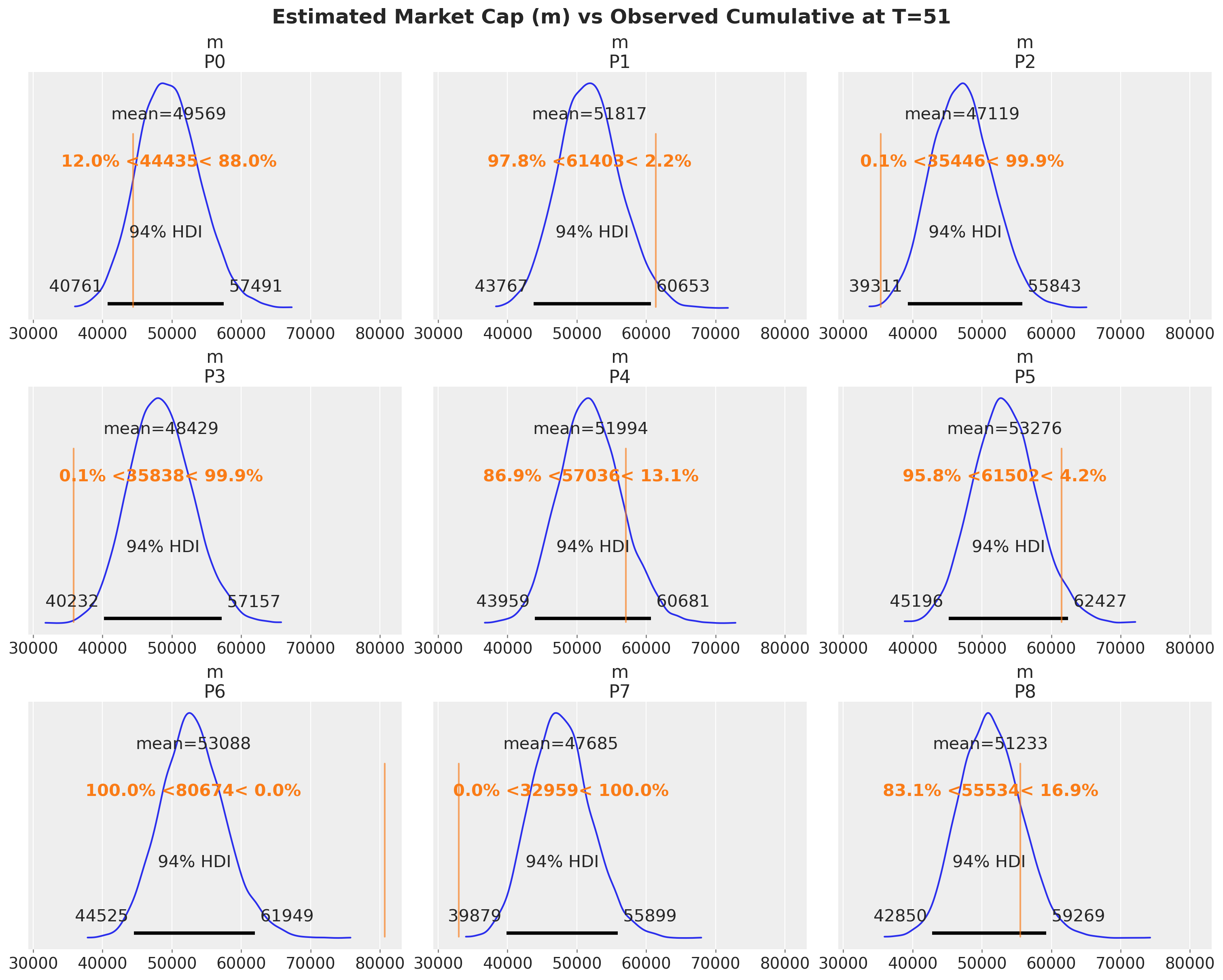
Overall, the model does a good job of capturing the data.

Next, we look into the adopters, which represent the expected value of the likelihood.

fig, axes = plt.subplots(
    nrows=3, ncols=3, figsize=(15, 12), sharex=True, sharey=True, layout="constrained"
)

idata["posterior"]["adopters"].pipe(plot_curve, {"T"}, axes=axes)

for i, ax in enumerate(axes.flatten()):
    ax.plot(T, bass_data[:, i], color="black")

fig.suptitle("Adopters vs Observed Data", fontsize=18, fontweight="bold");

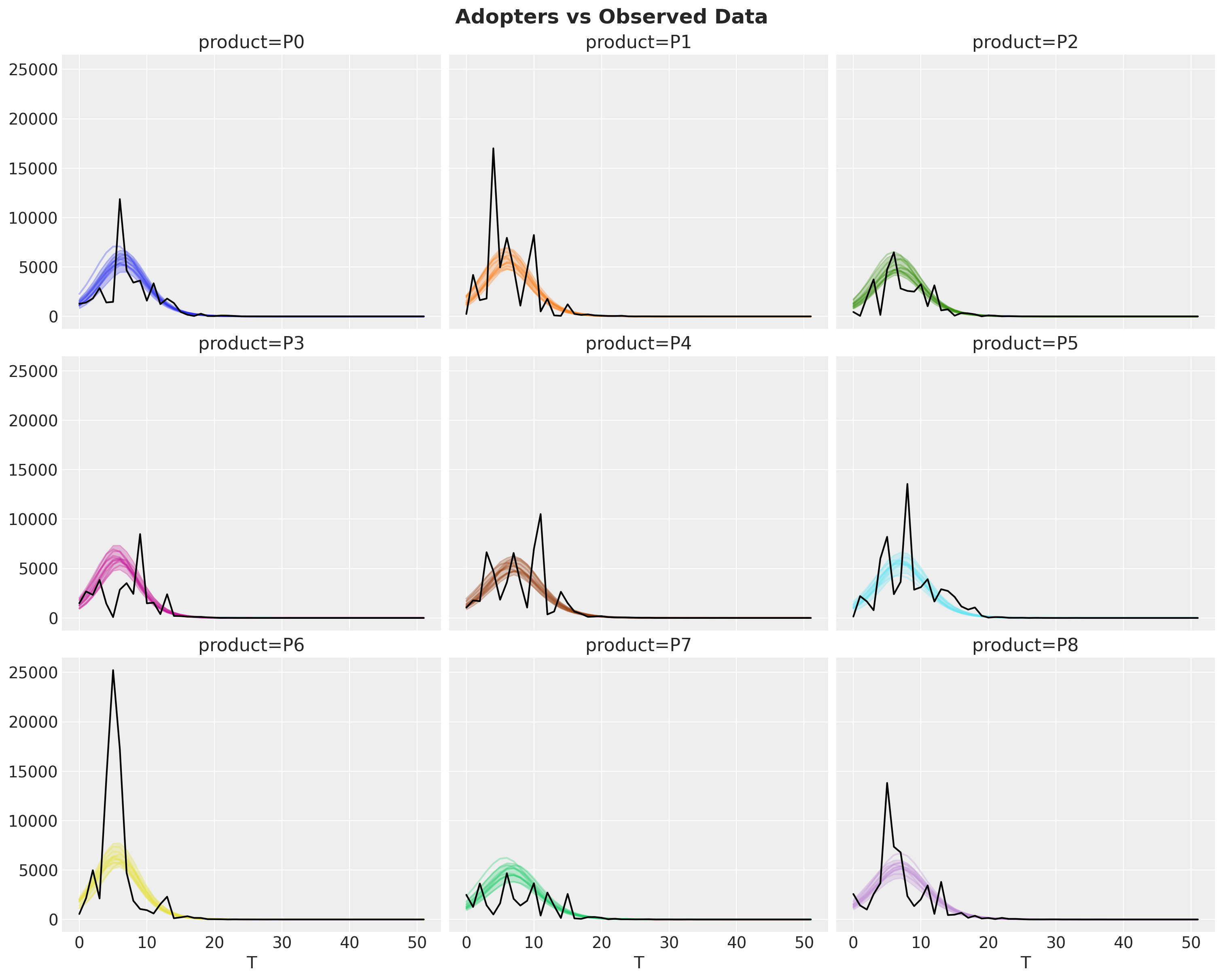
This show the fit is indeed quite reasonable.

We can also evaluate the model goodness by looking into the cumulative data:

Note

Remember that the adopters is the mean of the distribution so we see some cumulative curves above and some below.

Look at the idata["posterior_predictive"]["y"] for the observed data.

fig, axes = plt.subplots(
    nrows=3, ncols=3, figsize=(15, 12), sharex=True, sharey=True, layout="constrained"
)

idata["posterior"]["adopters"].cumsum(dim="T").pipe(plot_curve, {"T"}, axes=axes)

for i, ax in enumerate(axes.flatten()):
    ax.plot(T, bass_data[:, i].cumsum(), color="black")

fig.suptitle("Adopters Cumulative vs Observed Data", fontsize=18, fontweight="bold");

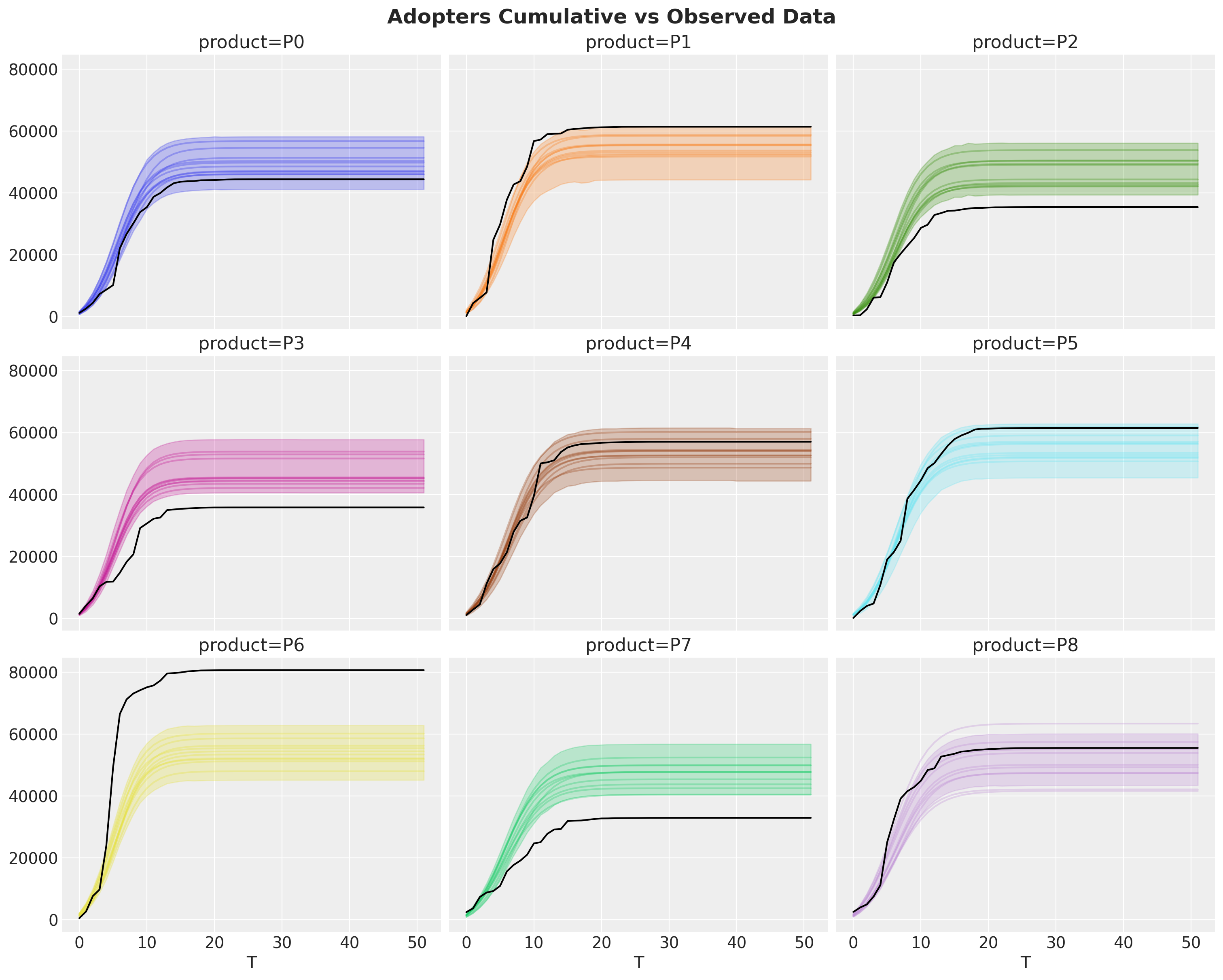
We can enhance this view by looking into the components of the model: innovators and imitators (in orange and green, respectively).

fig, axes = plt.subplots(
    nrows=3, ncols=3, figsize=(15, 12), sharex=True, sharey=True, layout="constrained"
)

idata["posterior"]["adopters"].cumsum(dim="T").pipe(
    plot_curve, {"T"}, colors=3 * 3 * ["C0"], axes=axes
)

idata["posterior"]["innovators"].pipe(
    plot_curve, {"T"}, colors=3 * 3 * ["C1"], axes=axes
)
idata["posterior"]["imitators"].pipe(
    plot_curve, {"T"}, colors=3 * 3 * ["C2"], axes=axes
)

for i, ax in enumerate(axes.flatten()):
    ax.plot(T, bass_data[:, i].cumsum(), color="black")

fig.suptitle("Innovators vs Imitators", fontsize=18, fontweight="bold");

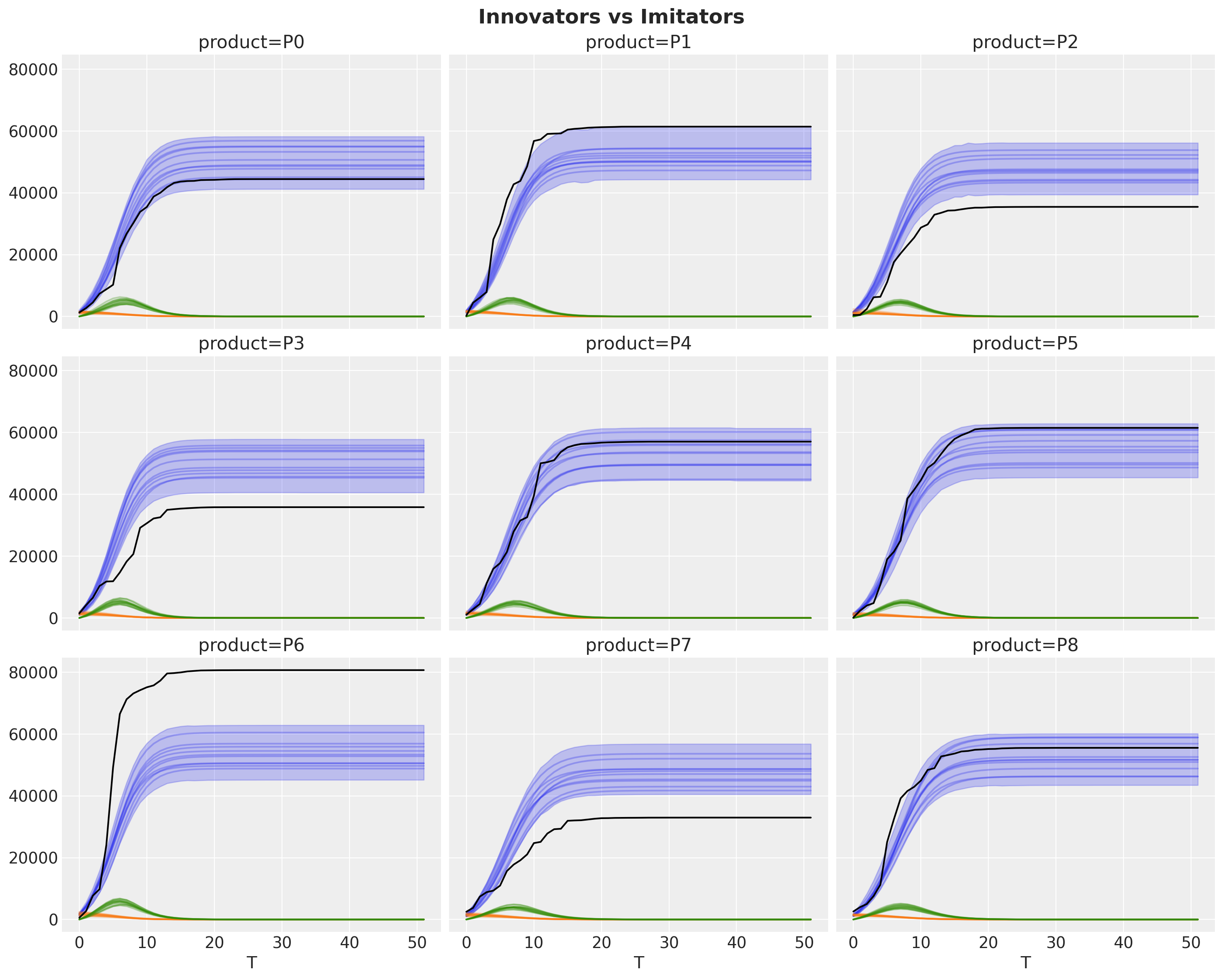
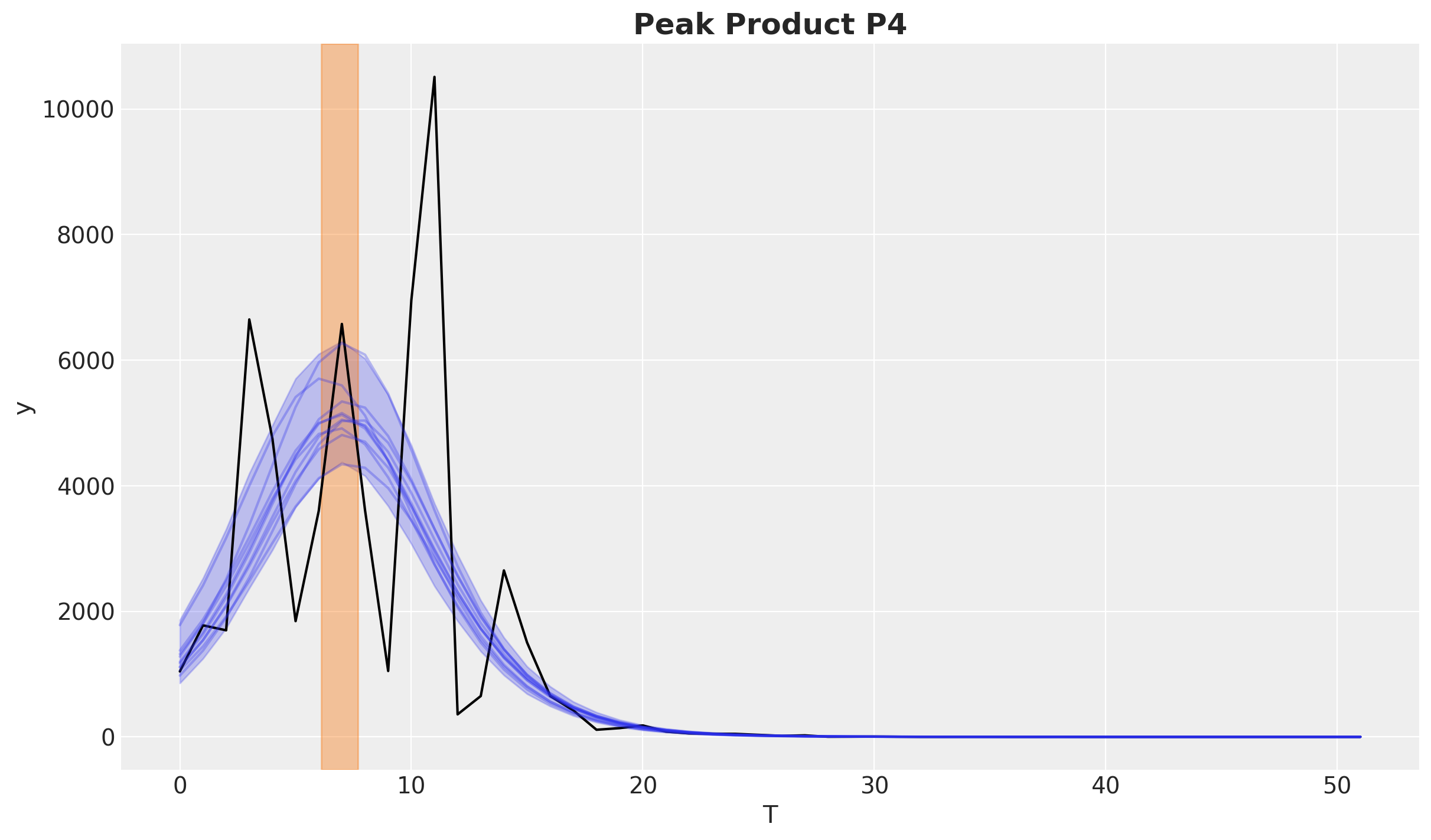
Finally, we can inspect the peak of the adoption curve.

ax, *_ = az.plot_forest(idata["posterior"]["peak"], combined=True)
ax.get_figure().suptitle("Peak", fontsize=18, fontweight="bold");

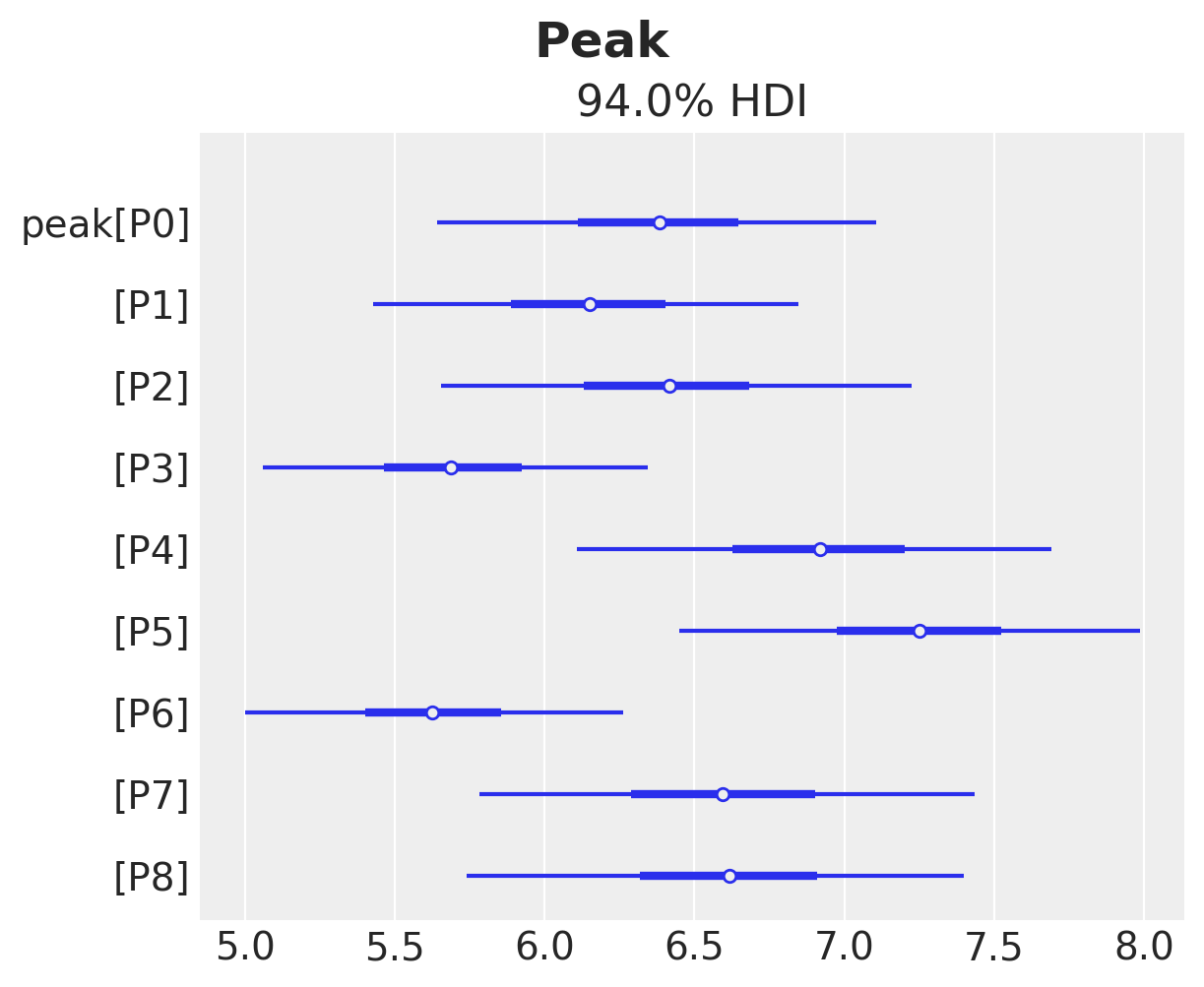
This fits the observed data quite well. Let’s see for example the product P4.

fig, ax = plt.subplots()

product_id = 4

bass_data[:, product_id].plot(ax=ax, color="black")

idata["posterior"]["adopters"].sel(product=f"P{product_id}").pipe(
    plot_curve, {"T"}, axes=ax
)

peak_hdi = az.hdi(idata["posterior"]["peak"].sel(product=f"P{product_id}"))["peak"]
ax.axvspan(
    peak_hdi.sel(hdi="lower").item(),
    peak_hdi.sel(hdi="higher").item(),
    color="C1",
    alpha=0.4,
)

ax.set_title(f"Peak Product {products[product_id]}", fontsize=18, fontweight="bold");

%load_ext watermark
%watermark -n -u -v -iv -w -p nutpie,pymc_marketing,pytensor

Last updated: Wed May 21 2025

Python implementation: CPython
Python version       : 3.10.16
IPython version      : 8.34.0

nutpie        : 0.14.3
pymc_marketing: 0.13.1
pytensor      : 2.30.3

pymc_marketing: 0.13.1
xarray        : 2025.3.1
arviz         : 0.21.0
numpy         : 1.26.4
pandas        : 2.2.3
matplotlib    : 3.10.1
pymc          : 5.22.0

Watermark: 2.5.0